Layout Optimization

The FLORIS package provides layout optimization tools to place turbines within a specified boundary area to optimize annual energy production (AEP) or wind plant value. Layout optimizers accept an instantiated FlorisModel and alter the turbine layouts in order to improve the objective function value (AEP or value).

Background

Layout optimization entails placing turbines in a wind farm in a configuration that maximizes an objective function, usually the AEP. Turbines are moved to minimize their wake interactions in the most dominant wind directions, while respecting the boundaries of the area for turbine placement as well as minimum distance requirements between neighboring turbines.

Mathematically, we represent this as a (nonconvex) optimization problem. Let \(x = \{x_i\}_{i=1,\dots,N}\), \(x_i \in \mathbb{R}^2\) represent the set of coordinates of turbines within a farm (that is, \(x_i\) represents the \((X, Y)\) location of turbine \(i\)). Further, let \(R \subset \mathbb{R}^2\) be a closed region in which to place turbines. Finally, let \(d\) represent the minimum allowable distance between two turbines. Then, the layout optimization problem is expressed as

\[\begin{split} \begin{aligned} \underset{x}{\text{maximize}} & \:\: f(x)\\ \text{subject to} & \:\: x \subset R \\ & \:\: ||x_i - x_j|| \geq d \:\: \forall j = 1,\dots,N, j\neq i \end{aligned} \end{split}\]

Here, \(||\cdot||\) denotes the Euclidean norm, and \(f(x)\) is the cost function to be maximized.

When maximizing the AEP, \(f = \sum_w P(w, x)p_W(w)\), where \(w\) is the wind condition bin (e.g., wind speed, wind direction pair); \(P(w, x)\) is the power produced by the wind farm in condition \(w\) with layout \(x\); and \(p_W(w)\) is the annual frequency of occurrence of condition \(w\).

Layout optimizers take iterative approaches to solving the layout optimization problem specified above. Optimization routines available in FLORIS are described below.

Scipy layout optimization

The LayoutOptimizationScipy class is built around scipy.optimizes minimize routine, using the SLSQP solver by default. Options for adjusting minimize's behavior are exposed to the user with the optOptions argument. Other options include enabling fast wake steering at each layout optimizer iteration with the enable_geometric_yaw argument, and switch from AEP optimization to value optimization with the use_value argument.

Genetic random search layout optimization

The LayoutOptimizationRandomSearch class is a custom optimizer designed specifically for layout optimization via random perturbations of the turbine locations. It is designed to have the following features:

• Robust to complex wind conditions and complex boundaries, including disjoint regions for turbine placement

• Easy to parallelize and wrapped in a genetic algorithm for propagating candidate solutions

• Simple to set up and tune for non-optimization experts

• Set up to run cheap constraint checks prior to more expensive objective function evaluations to accelerate optimization

The algorithm, described in full in Sinner and Fleming [1], moves a random turbine and random distance in a random direction; checks that constraints are satisfied; evaluates the objective function (AEP or value); and then commits to the move if there is an objective function improvement. The main tuning parameter is the probability mass function for the random movement distance, which is a dictionary to be passed to the distance_pmf argument.

The distance_pmf dictionary should contain two keys, each containing a 1D array of equal length: "d", which specifies the perturbation distance in units of the rotor diameter, and "p", which specifies the probability that the corresponding perturbation distance is chosen at any iteration of the random search algorithm. The distance_pmf can therefore be used to encourage or discourage more aggressive or more conservative movements, and to enable or disable jumps between disjoint regions for turbine placement.

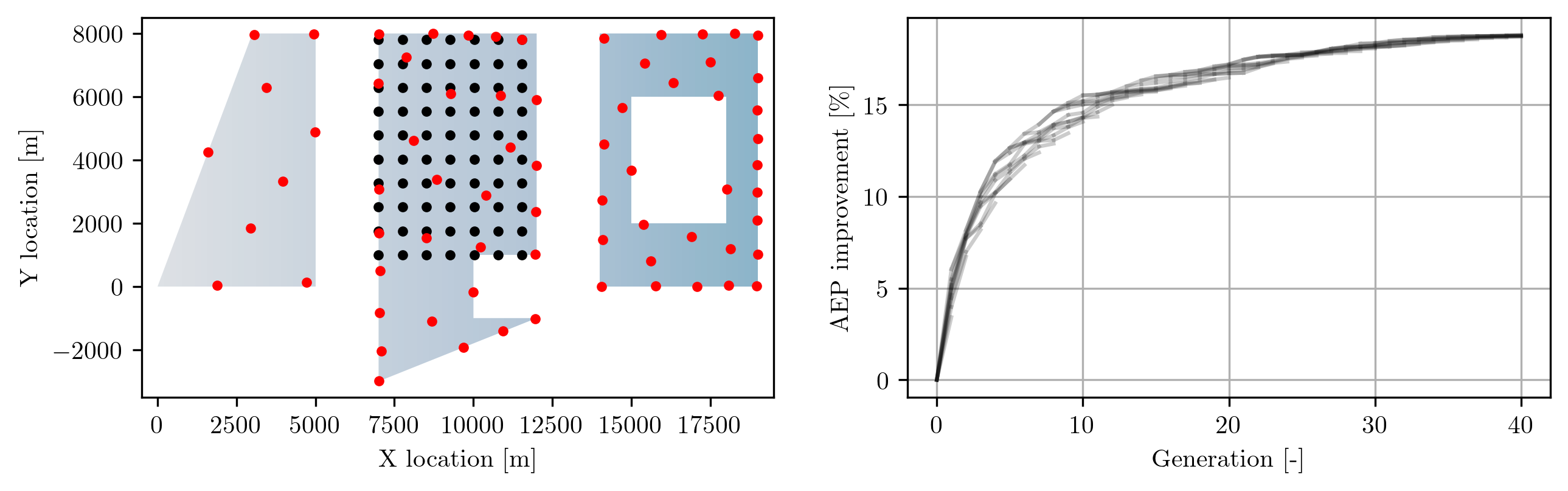
The figure below shows an example of the optimized layout of a farm using the GRS algorithm, with the black dots indicating the initial layout; red dots indicating the final layout; and blue shading indicating wind speed heterogeneity (lighter shade is lower wind speed, darker shade is higher wind speed). The progress of each of the genetic individuals in the optimization process is shown in the right-hand plot.

Gridded layout optimization

The LayoutOptimizationGridded class allows users to quickly find a layout that fits the most turbines possible into the specified boundary area, given that the turbines are arranged in a gridded layout. To do so, a range of different rotations and translations of a generic gridded arrangement are tried, and the one that fits the most turbines into the boundary area is selected. No AEP evaluations are performed; rather, the cost function \(f\) to be maximized is simply \(N\), the number of turbines, and there is an additional constraint that the turbines are arranged in a gridded fashion. Note that in other layout optimizers, \(N\) is fixed.

We envisage that this will be useful for users that want to quickly generate a layout to "fill" a boundary region in a gridded manner. By default, the gridded arrangement is a square grid with spacing of min_dist (or min_dist_D); however, instantiating with the hexagonal_packing keyword argument set to True will provide a grid that offsets the rows to enable tighter packing of turbines while still satisfying the min_dist.

As with the LayoutOptimizationRandomSearch class, the boundaries specified can be complex (and may contain separate areas). User settings include rotation_step, which specifies the step size for rotating the grid (in degrees); rotation_range, which specifies the range of rotation angles; translation_step or translation_step_D, which specifies the step size for translating the grid in meters or rotor diameters, respectively; and translation_range, which specifies the range of possible translations. All come with default values, which we expect to be suitable for many or most users.