LETID - Passivated Wafer#
This example shows how to simulate an accelerated test performed on a well-passivated Si wafer, rather than a solar cell. In a well-passivated wafer, carrier injection (\(\Delta n\)) is linearly proportional to carrier lifetime, assuming surface recombination velocity can be approximated to be zero.
LETID and boron-oxygen LID defect transitions are known to accelerate with increased carrier injection, by term \(\Delta n^{x_{ij}}\), where \(x_{ij}\) is different for each transition \(i \rightarrow j\) and is related to the stoichiometric involvement of excess carriers in the defect reaction.
Requirements:
pandas,numpy,matplotlib,scipy
Objectives:
Define necessary wafer device parameters
Define necessary degradation parameters: degraded lifetime and defect states
Create timeseries of temperature and injection
Run through timeseries, calculating defect states
Calculate device degradation and plot
# if running on google colab, uncomment the next line and execute this cell to install the dependencies and prevent "ModuleNotFoundError" in later cells:
# !pip install pvdeg==0.3.3
from pvdeg import letid, collection, utilities, DATA_DIR
import pvdeg
import os
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# This information helps with debugging and getting support :)
import sys, platform
print("Working on a ", platform.system(), platform.release())
print("Python version ", sys.version)
print("Pandas version ", pd.__version__)
print("pvdeg version ", pvdeg.__version__)
Working on a Linux 6.5.0-1025-azure
Python version 3.11.9 (main, Jul 15 2024, 21:50:21) [GCC 11.4.0]
Pandas version 2.2.2
pvdeg version 0.1.dev1+g4f38099
Device parameters#
For modeling a wafer, we don’t need as many device parameters. Wafer thickness, lifetime, and an optical generation profile, which allows us to calculate generation current, which we take to be device current assuming surface recombination is very low.
wafer_thickness = 180 # um
tau = 350 # us, lifetime of the wafer for demonstration purposes
generation_df = pd.read_excel(os.path.join(DATA_DIR, 'PVL_GenProfile.xlsx'), header = 0) # this is an optical generation profile generated by PVLighthouse's OPAL2 default model for 1-sun, normal incident AM1.5 sunlight on a 180-um thick SiNx-coated, pyramid-textured wafer.
generation = generation_df['Generation (cm-3s-1)']
depth = generation_df['Depth (um)']
j_gen = collection.generation_current(generation, depth)
Degradation parameters#
Here we’ll model LETID under 0.5-sun, open-circuit injection. In a passivated wafer, recombination per volume (\(\frac{\Delta n}{\tau}\)) must equal generation per volume (\(\frac{Jq}{W}\)), which gives \(\Delta n = \frac{Jq\tau}{W}\)
The term \(\Delta n^{x_{ij}}\) is calculated for wafers by the function letid.carrier_factor_wafer, which adjusts the rate of the transition \(i \rightarrow j\) for \(\Delta n\).
Since kinetic parameters are taken from literature that may have used different \(\Delta n\), we adjust transitions by the ratio \(\frac{\Delta n}{\Delta n_{lit}}\).
See Repins et al. 2023 for more details.
mechanism_params = utilities.get_kinetics('repins')
injection = 0.5 #
Demonstrate calculation of dn^x_ij#
Calculate \(\Delta n\) of the wafer
from scipy.constants import elementary_charge as q # Elementary charge, C
dn = (((j_gen * 0.001 * 10000 * injection) * (tau * 1e-6))/ (wafer_thickness * 1e-6)/ q) # calculate excess carrier density
dn
2.57051594134322e+21
Calculate \(\Delta n_{lit}\), the excess carrier density from the literature experiments where kinetic parameters were determined. Assuming literature experiments were carried out on cells, this requires using the
calc_dnfunction
from scipy.constants import convert_temperature
transition = 'bc' # for this example we'll look at the B -> C transition
meas_tau = mechanism_params[f"tau_{transition}"]
meas_temp = mechanism_params[f"temperature_{transition}"]
meas_temp = convert_temperature(meas_temp, 'K', 'C')
meas_suns = mechanism_params[f"suns_{transition}"]
meas_jsc = 40
meas_wafer_thickness = mechanism_params[f"thickness_{transition}"]
meas_srv = mechanism_params[f"srv_{transition}"]
meas_structure = mechanism_params[f"structure_{transition}"]
dn_lit = letid.calc_dn(
meas_tau,
meas_temp,
meas_suns,
meas_jsc,
wafer_thickness=meas_wafer_thickness,
s_rear=meas_srv,
)
dn_lit
7.064647199192719e+20
Return the exponent \(x_{ij}\) of the transition in question
exponent = mechanism_params[f"x_{transition}"]
exponent
1.2
Calculate \((\frac{\Delta n}{\Delta n_{lit}})^{x_{ij}}\). This is the acceleration factor of the transition due to excess carriers.
(dn/dn_lit)**exponent
4.711029107876425
# the "carrier_factor_wafer" function yields the same result
letid.carrier_factor_wafer(tau, transition, injection, j_gen, wafer_thickness, mechanism_params)
4.711029107876425
Degradation parameters#
To model the device’s degradation, we need to define several more important quantities about the degradation the device will experience. These include undegraded and degraded lifetime (in \(\mu s\)), and starting defect state percentages
tau_0 = 350 # us, carrier lifetime in non-degraded states, e.g. LETID/LID states A or C
tau_deg = 41 # us, carrier lifetime in fully-degraded state, e.g. LETID/LID state B
# starting defect state percentages
nA_0 = 100
nB_0 = 0
nC_0 = 0
mechanism_params = utilities.get_kinetics('repins')
print(mechanism_params)
{'mechanism': 'LETID', 'v_ab': 46700000.0, 'v_ba': 4.7e-25, 'v_bc': 19900000.0, 'v_cb': 0.0, 'ea_ab': 0.827, 'ea_ba': -1.15, 'ea_bc': 0.871, 'ea_cb': 0.0, 'suns_ab': 1.0, 'suns_bc': 1.0, 'temperature_ab': 410, 'temperature_bc': 410, 'tau_ab': 75, 'tau_bc': 75, 'x_ab': 1, 'x_ba': 1.7, 'x_bc': 1.2, 'structure_ab': 'cell', 'structure_bc': 'cell', 'thickness_ab': 200, 'thickness_bc': 200, 'srv_ab': 90, 'srv_bc': 90, 'doi': 'doi:10.1557/s43577-022-00438-8', 'comments': ''}
Set up timeseries#
In this example, we are going to model a wafer exposed to 0.5 suns illumination at \(125\degree C\) for 24 hours, and compare to experimental data from Wyller et al. 2021.
temperature = 125 # degrees celsius
suns = 0.5 # "suns" of injection, e.g 1-sun illumination at open circuit would be 1; dark current injection is given as a fraction of Isc, e.g., injecting Isc would be 1. For this example we assume injection is 0.1*Isc.
timesteps = pd.date_range(start = '2022-01-01 00:00:00', end = '2022-01-02 00:00:00', freq = 'S') # three weeks of 1-minute interval timesteps. In general, we should select small timesteps unless we are sure defect reactions are proceeding very slowly
timesteps = pd.DataFrame(timesteps, columns = ['Datetime'])
temps = np.full(len(timesteps), temperature)
injection = np.full(len(timesteps), suns)
timesteps['Temperature'] = temps
timesteps['Injection'] = injection
timesteps[['NA', 'NB', 'NC', 'tau']] = np.nan # create columns for defect state percentages and lifetime, fill with NaNs for now, to fill iteratively below
timesteps.loc[0, ['NA', 'NB', 'NC']] = nA_0, nB_0, nC_0 # assign first timestep defect state percentages
timesteps.loc[0, 'tau'] = letid.tau_now(tau_0, tau_deg, nB_0) # calculate tau for the first timestep
/tmp/ipykernel_2272/530898593.py:4: FutureWarning: 'S' is deprecated and will be removed in a future version, please use 's' instead.
timesteps = pd.date_range(start = '2022-01-01 00:00:00', end = '2022-01-02 00:00:00', freq = 'S') # three weeks of 1-minute interval timesteps. In general, we should select small timesteps unless we are sure defect reactions are proceeding very slowly
timesteps
| Datetime | Temperature | Injection | NA | NB | NC | tau | |
|---|---|---|---|---|---|---|---|
| 0 | 2022-01-01 00:00:00 | 125 | 0.5 | 100.0 | 0.0 | 0.0 | 350.0 |
| 1 | 2022-01-01 00:00:01 | 125 | 0.5 | NaN | NaN | NaN | NaN |
| 2 | 2022-01-01 00:00:02 | 125 | 0.5 | NaN | NaN | NaN | NaN |
| 3 | 2022-01-01 00:00:03 | 125 | 0.5 | NaN | NaN | NaN | NaN |
| 4 | 2022-01-01 00:00:04 | 125 | 0.5 | NaN | NaN | NaN | NaN |
| ... | ... | ... | ... | ... | ... | ... | ... |
| 86396 | 2022-01-01 23:59:56 | 125 | 0.5 | NaN | NaN | NaN | NaN |
| 86397 | 2022-01-01 23:59:57 | 125 | 0.5 | NaN | NaN | NaN | NaN |
| 86398 | 2022-01-01 23:59:58 | 125 | 0.5 | NaN | NaN | NaN | NaN |
| 86399 | 2022-01-01 23:59:59 | 125 | 0.5 | NaN | NaN | NaN | NaN |
| 86400 | 2022-01-02 00:00:00 | 125 | 0.5 | NaN | NaN | NaN | NaN |
86401 rows × 7 columns
Run through timesteps#
Since each timestep depends on the preceding timestep, we need to calculate in a loop. This will take a few minutes depending on the length of the timeseries.
for index, timestep in timesteps.iterrows():
# first row tau has already been assigned
if index == 0:
pass
# loop through rows, new tau calculated based on previous NB. Reaction proceeds based on new tau.
else:
n_A = timesteps.at[index-1, 'NA']
n_B = timesteps.at[index-1, 'NB']
n_C = timesteps.at[index-1, 'NC']
tau = letid.tau_now(tau_0, tau_deg, n_B)
j_gen = j_gen
temperature = timesteps.at[index, 'Temperature']
injection = timesteps.at[index, 'Injection']
# calculate defect reaction kinetics: reaction constant and carrier concentration factor.
k_AB = letid.k_ij(mechanism_params['v_ab'], mechanism_params['ea_ab'], temperature)
k_BA = letid.k_ij(mechanism_params['v_ba'], mechanism_params['ea_ba'], temperature)
k_BC = letid.k_ij(mechanism_params['v_bc'], mechanism_params['ea_bc'], temperature)
k_CB = letid.k_ij(mechanism_params['v_cb'], mechanism_params['ea_cb'], temperature)
x_ab = letid.carrier_factor_wafer(tau, 'ab', injection, j_gen, wafer_thickness, mechanism_params)
x_ba = letid.carrier_factor_wafer(tau, 'ba', injection, j_gen, wafer_thickness, mechanism_params)
x_bc = letid.carrier_factor_wafer(tau, 'bc', injection, j_gen, wafer_thickness, mechanism_params)
# x_cb there is no known excess carrier acceleration factor for the c->b transition
# calculate the instantaneous change in NA, NB, and NC
dN_Adt = (k_BA * n_B * x_ba) - (k_AB * n_A * x_ab)
dN_Bdt = (k_AB * n_A * x_ab) + (k_CB * n_C) - ((k_BA * x_ba + k_BC * x_bc) * n_B)
dN_Cdt = (k_BC * n_B * x_bc) - (k_CB * n_C)
t_step = (timesteps.at[index, 'Datetime'] - timesteps.at[index-1,'Datetime']).total_seconds()
# assign new defect state percentages
timesteps.at[index, 'NA'] = n_A + dN_Adt*t_step
timesteps.at[index, 'NB'] = n_B + dN_Bdt*t_step
timesteps.at[index, 'NC'] = n_C + dN_Cdt*t_step
Finish calculating degraded device parameters.#
Now that we have calculated defect states, we can calculate all the quantities that depend on defect states. Since this is a wafer, device parameters like Jsc, Voc, FF, etc., aren’t really appropriate
For wafers, results are often presented in terms of normalized defect density (NDD), where
\(NDD(t) = \frac{1}{\tau (t)} - \frac{1}{\tau _0}\)
timesteps['tau'] = letid.tau_now(tau_0, tau_deg, timesteps['NB'])
timesteps['NDD'] = letid.calc_ndd(timesteps['tau'].iloc[0], timesteps['tau'])
timesteps['time (s)'] = (timesteps['Datetime'] - timesteps.iloc[0]['Datetime']).dt.total_seconds() # create a column for seconds elapsed
timesteps
| Datetime | Temperature | Injection | NA | NB | NC | tau | NDD | time (s) | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 2022-01-01 00:00:00 | 125 | 0.5 | 1.000000e+02 | 0.000000e+00 | 0.000000 | 350.000000 | 0.000000 | 0.0 |
| 1 | 2022-01-01 00:00:01 | 125 | 0.5 | 9.942178e+01 | 5.782160e-01 | 0.000000 | 335.384693 | 0.000125 | 1.0 |
| 2 | 2022-01-01 00:00:02 | 125 | 0.5 | 9.887092e+01 | 1.128597e+00 | 0.000486 | 322.563499 | 0.000243 | 2.0 |
| 3 | 2022-01-01 00:00:03 | 125 | 0.5 | 9.834404e+01 | 1.654564e+00 | 0.001392 | 311.194745 | 0.000356 | 3.0 |
| 4 | 2022-01-01 00:00:04 | 125 | 0.5 | 9.783845e+01 | 2.158887e+00 | 0.002663 | 301.021824 | 0.000465 | 4.0 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 86396 | 2022-01-01 23:59:56 | 125 | 0.5 | 5.800845e-34 | 3.370010e-27 | 100.000000 | 350.000000 | 0.000000 | 86396.0 |
| 86397 | 2022-01-01 23:59:57 | 125 | 0.5 | 5.795712e-34 | 3.367028e-27 | 100.000000 | 350.000000 | 0.000000 | 86397.0 |
| 86398 | 2022-01-01 23:59:58 | 125 | 0.5 | 5.790584e-34 | 3.364048e-27 | 100.000000 | 350.000000 | 0.000000 | 86398.0 |
| 86399 | 2022-01-01 23:59:59 | 125 | 0.5 | 5.785460e-34 | 3.361072e-27 | 100.000000 | 350.000000 | 0.000000 | 86399.0 |
| 86400 | 2022-01-02 00:00:00 | 125 | 0.5 | 5.780341e-34 | 3.358098e-27 | 100.000000 | 350.000000 | 0.000000 | 86400.0 |
86401 rows × 9 columns
Plot the results#
from cycler import cycler
plt.style.use('default')
fig, ax = plt.subplots()
ax.set_prop_cycle(cycler('color', ['tab:blue', 'tab:orange', 'tab:green']) + cycler('linestyle', ['-', '--', '-.']))
ax.plot(timesteps['time (s)'], timesteps[['NA', 'NB', 'NC']].values)
ax.legend(labels = ['$N_A$', '$N_B$', '$N_C$'], loc = 'upper left')
ax.set_ylabel('Defect state percentages [%]')
ax.set_xlabel('Time [s]')
ax2 = ax.twinx()
c_norm = 1.35 #Normalization constants "C_norm". See Repins 2023 for details
ax2.plot(timesteps['time (s)'], timesteps['NDD']*c_norm, c = 'black', label = 'NDD modeled')
ax.set_ylabel('NDD [$\mu s^{-1}$]')
literature_data_file = os.path.join(DATA_DIR, 'wyller data.csv')
data = pd.read_csv(literature_data_file, header = 0)
filtered = data[data['Series'] == '0.5 sun 125C']
ax2.scatter(filtered['X'], filtered['Y'], label = 'NDD data from Wyller', marker = 'v', c = 'black')
ax2.legend(loc = 'center left')
ax.set_xscale('log')
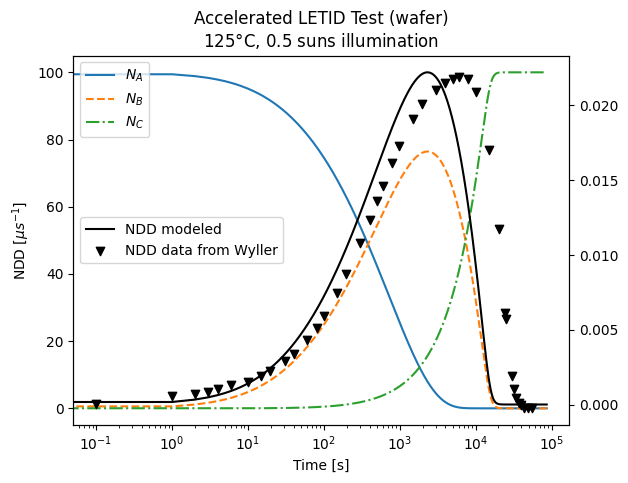
ax.set_title('Accelerated LETID Test (wafer)\n'fr'{temperature}$\degree$C, {suns} suns illumination')
plt.show()
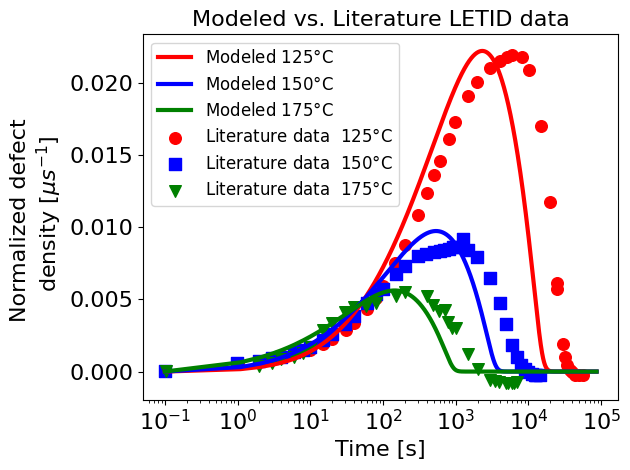
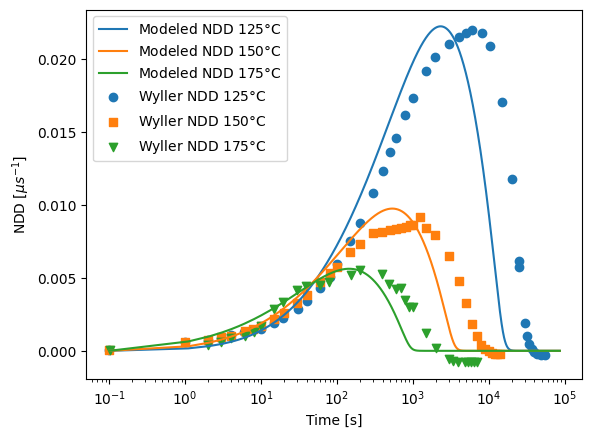
Compare model results to experimental data#
Experimental data (0.5 suns, 125°C, 150°C, 175°C) from Wyller 2021. Comparison with experimental data requires normalization constant (\(C_{norm}\)), which relates NDD to \(N_B\) as described in Repins 2023.
temperatures = [125, 150, 175] # degrees celsius
timesteps125 = timesteps #we already modeled the 125C experiment above
temperature = temperatures[1] # degrees celsius
suns = 0.5 # "suns" of injection, e.g 1-sun illumination at open circuit would be 1; dark current injection is given as a fraction of Isc, e.g., injecting Isc would be 1. For this example we assume injection is 0.1*Isc.
timesteps = pd.date_range(start = '2022-01-01 00:00:00', end = '2022-01-02 00:00:00', freq = 'S') # three weeks of 1-minute interval timesteps. In general, we should select small timesteps unless we are sure defect reactions are proceeding very slowly
timesteps = pd.DataFrame(timesteps, columns = ['Datetime'])
temps = np.full(len(timesteps), temperature)
injection = np.full(len(timesteps), suns)
timesteps['Temperature'] = temps
timesteps['Injection'] = injection
timesteps[['NA', 'NB', 'NC', 'tau']] = np.nan # create columns for defect state percentages and lifetime, fill with NaNs for now, to fill iteratively below
timesteps.loc[0, ['NA', 'NB', 'NC']] = nA_0, nB_0, nC_0 # assign first timestep defect state percentages
timesteps.loc[0, 'tau'] = letid.tau_now(tau_0, tau_deg, nB_0) # calculate tau for the first timestep
/tmp/ipykernel_2272/241191725.py:4: FutureWarning: 'S' is deprecated and will be removed in a future version, please use 's' instead.
timesteps = pd.date_range(start = '2022-01-01 00:00:00', end = '2022-01-02 00:00:00', freq = 'S') # three weeks of 1-minute interval timesteps. In general, we should select small timesteps unless we are sure defect reactions are proceeding very slowly
for index, timestep in timesteps.iterrows():
# first row tau has already been assigned
if index == 0:
pass
# loop through rows, new tau calculated based on previous NB. Reaction proceeds based on new tau.
else:
n_A = timesteps.at[index-1, 'NA']
n_B = timesteps.at[index-1, 'NB']
n_C = timesteps.at[index-1, 'NC']
tau = letid.tau_now(tau_0, tau_deg, n_B)
j_gen = j_gen
temperature = timesteps.at[index, 'Temperature']
injection = timesteps.at[index, 'Injection']
# calculate defect reaction kinetics: reaction constant and carrier concentration factor.
k_AB = letid.k_ij(mechanism_params['v_ab'], mechanism_params['ea_ab'], temperature)
k_BA = letid.k_ij(mechanism_params['v_ba'], mechanism_params['ea_ba'], temperature)
k_BC = letid.k_ij(mechanism_params['v_bc'], mechanism_params['ea_bc'], temperature)
k_CB = letid.k_ij(mechanism_params['v_cb'], mechanism_params['ea_cb'], temperature)
x_ab = letid.carrier_factor_wafer(tau, 'ab', injection, j_gen, wafer_thickness, mechanism_params)
x_ba = letid.carrier_factor_wafer(tau, 'ba', injection, j_gen, wafer_thickness, mechanism_params)
x_bc = letid.carrier_factor_wafer(tau, 'bc', injection, j_gen, wafer_thickness, mechanism_params)
# x_cb there is no known excess carrier acceleration factor for the c->b transition
# calculate the instantaneous change in NA, NB, and NC
dN_Adt = (k_BA * n_B * x_ba) - (k_AB * n_A * x_ab)
dN_Bdt = (k_AB * n_A * x_ab) + (k_CB * n_C) - ((k_BA * x_ba + k_BC * x_bc) * n_B)
dN_Cdt = (k_BC * n_B * x_bc) - (k_CB * n_C)
t_step = (timesteps.at[index, 'Datetime'] - timesteps.at[index-1,'Datetime']).total_seconds()
# assign new defect state percentages
timesteps.at[index, 'NA'] = n_A + dN_Adt*t_step
timesteps.at[index, 'NB'] = n_B + dN_Bdt*t_step
timesteps.at[index, 'NC'] = n_C + dN_Cdt*t_step
timesteps['tau'] = letid.tau_now(tau_0, tau_deg, timesteps['NB'])
timesteps['NDD'] = letid.calc_ndd(timesteps['tau'].iloc[0], timesteps['tau'])
timesteps['time (s)'] = (timesteps['Datetime'] - timesteps.iloc[0]['Datetime']).dt.total_seconds() # create a column for seconds elapsed
timesteps150 = timesteps
temperature = temperatures[2] # degrees celsius
suns = 0.5 # "suns" of injection, e.g 1-sun illumination at open circuit would be 1; dark current injection is given as a fraction of Isc, e.g., injecting Isc would be 1. For this example we assume injection is 0.1*Isc.
timesteps = pd.date_range(start = '2022-01-01 00:00:00', end = '2022-01-02 00:00:00', freq = 'S') # three weeks of 1-minute interval timesteps. In general, we should select small timesteps unless we are sure defect reactions are proceeding very slowly
timesteps = pd.DataFrame(timesteps, columns = ['Datetime'])
temps = np.full(len(timesteps), temperature)
injection = np.full(len(timesteps), suns)
timesteps['Temperature'] = temps
timesteps['Injection'] = injection
timesteps[['NA', 'NB', 'NC', 'tau']] = np.nan # create columns for defect state percentages and lifetime, fill with NaNs for now, to fill iteratively below
timesteps.loc[0, ['NA', 'NB', 'NC']] = nA_0, nB_0, nC_0 # assign first timestep defect state percentages
timesteps.loc[0, 'tau'] = letid.tau_now(tau_0, tau_deg, nB_0) # calculate tau for the first timestep
/tmp/ipykernel_2272/950821369.py:4: FutureWarning: 'S' is deprecated and will be removed in a future version, please use 's' instead.
timesteps = pd.date_range(start = '2022-01-01 00:00:00', end = '2022-01-02 00:00:00', freq = 'S') # three weeks of 1-minute interval timesteps. In general, we should select small timesteps unless we are sure defect reactions are proceeding very slowly
for index, timestep in timesteps.iterrows():
# first row tau has already been assigned
if index == 0:
pass
# loop through rows, new tau calculated based on previous NB. Reaction proceeds based on new tau.
else:
n_A = timesteps.at[index-1, 'NA']
n_B = timesteps.at[index-1, 'NB']
n_C = timesteps.at[index-1, 'NC']
tau = letid.tau_now(tau_0, tau_deg, n_B)
j_gen = j_gen
temperature = timesteps.at[index, 'Temperature']
injection = timesteps.at[index, 'Injection']
# calculate defect reaction kinetics: reaction constant and carrier concentration factor.
k_AB = letid.k_ij(mechanism_params['v_ab'], mechanism_params['ea_ab'], temperature)
k_BA = letid.k_ij(mechanism_params['v_ba'], mechanism_params['ea_ba'], temperature)
k_BC = letid.k_ij(mechanism_params['v_bc'], mechanism_params['ea_bc'], temperature)
k_CB = letid.k_ij(mechanism_params['v_cb'], mechanism_params['ea_cb'], temperature)
x_ab = letid.carrier_factor_wafer(tau, 'ab', injection, j_gen, wafer_thickness, mechanism_params)
x_ba = letid.carrier_factor_wafer(tau, 'ba', injection, j_gen, wafer_thickness, mechanism_params)
x_bc = letid.carrier_factor_wafer(tau, 'bc', injection, j_gen, wafer_thickness, mechanism_params)
# x_cb there is no known excess carrier acceleration factor for the c->b transition
# calculate the instantaneous change in NA, NB, and NC
dN_Adt = (k_BA * n_B * x_ba) - (k_AB * n_A * x_ab)
dN_Bdt = (k_AB * n_A * x_ab) + (k_CB * n_C) - ((k_BA * x_ba + k_BC * x_bc) * n_B)
dN_Cdt = (k_BC * n_B * x_bc) - (k_CB * n_C)
t_step = (timesteps.at[index, 'Datetime'] - timesteps.at[index-1,'Datetime']).total_seconds()
# assign new defect state percentages
timesteps.at[index, 'NA'] = n_A + dN_Adt*t_step
timesteps.at[index, 'NB'] = n_B + dN_Bdt*t_step
timesteps.at[index, 'NC'] = n_C + dN_Cdt*t_step
timesteps['tau'] = letid.tau_now(tau_0, tau_deg, timesteps['NB'])
timesteps['NDD'] = letid.calc_ndd(timesteps['tau'].iloc[0], timesteps['tau'])
timesteps['time (s)'] = (timesteps['Datetime'] - timesteps.iloc[0]['Datetime']).dt.total_seconds() # create a column for seconds elapsed
timesteps175 = timesteps
timesteps = pd.concat([timesteps125, timesteps150, timesteps175])
normalization_constants = {125 : 1.35, 150 : 0.6, 175 : 0.35} #Normalization constants "C_norm". See Repins 2023 for details
timesteps['Normalization constant'] = timesteps['Temperature'].map(normalization_constants)
timesteps['NDD-normalized'] = timesteps['NDD']*timesteps['Normalization constant']
grouped_model = timesteps.groupby('Temperature')
literature_data_file = os.path.join(DATA_DIR, 'wyller data.csv')
data = pd.read_csv(literature_data_file, header = 0)
data['Temperature'] = pd.to_numeric(data['Series'].str[-4:-1])
#normalization_constants = {'0.5 sun 125C' : 1/1.35, '0.5 sun 150C' : 1/0.6, '0.5 sun 175C' : 1/0.35}
#data['Normalization constant'] = data['Series'].map(normalization_constants)
#data['Y-normalized'] = data['Y']*data['Normalization constant']
grouped_data = data.groupby('Temperature')
import itertools
fig, ax = plt.subplots()
for name, group in grouped_model:
ax.plot(group['time (s)']+.1, group['NDD-normalized'], label = f"Modeled NDD {name}$\degree$C")
ax.legend()
marker = itertools.cycle(('o', 's', 'v', 'o', '*'))
for name, group in grouped_data:
ax.scatter(group['X'], group['Y'], label = f"Wyller NDD {name}$\degree$C", marker = next(marker))
ax.legend()
ax.set_xscale('log')
ax.set_xlabel('Time [s]')
ax.set_ylabel('NDD [$\mu s^{-1}$]')
plt.show()
import itertools
fig, ax = plt.subplots()
colors = itertools.cycle(('red', 'blue', 'green'))
for name, group in grouped_model:
ax.plot(group['time (s)']+.1, group['NDD-normalized'], color = next(colors), label = f"Modeled {name}$\degree$C", linewidth = 3)
ax.legend(prop={'size': 12})
marker = itertools.cycle(('o', 's', 'v', 'o', '*'))
for name, group in grouped_data:
ax.scatter(group['X'], group['Y'], label = f"Literature data {name}$\degree$C", color = next(colors), marker = next(marker), s = 70)
ax.legend(prop={'size': 12})
ax.set_xscale('log')
ax.tick_params(axis='both', which='major', labelsize=16)
ax.set_xlabel('Time [s]', fontsize = 16)
ax.set_ylabel('Normalized defect \n density [$\mu s^{-1}$]', fontsize = 16)
ax.set_title('Modeled vs. Literature LETID data', fontsize = 16)
plt.tight_layout()
#fig.savefig('wafer data.png', dpi = 600)
plt.show()
