LETID - Outdoor Scenario Based on Accelerated Test#
This is an example for using a test result to model LETID progression in outdoor environments
One important use case for this library is to use data from a LETID test (e.g. IEC TS 63342) to model how a module may degrade and regenerate in the field.
We will take some data from module testing presented in Karas et al. 2022, and use it to estimate device parameters.
We can use the equations in this library to model LETID progression in a simulated outdoor environment, given that we have weather and system data. This example makes use of tools from the fabulous pvlib library to calculate system irradiance and temperature, which we use to calculate progression in LETID states.
Requirements:
pvlib,pandas,numpy,matplotlib,scipy
Objectives:
Load data from example test results
Use
pvliband provided weather files to set up a temperature and injection timeseriesDefine necessary solar cell device parameters
Define necessary degradation parameters: degraded lifetime and defect states
Run through timeseries, calculating defect states
Calculate device degradation and plot
# if running on google colab, uncomment the next line and execute this cell to install the dependencies and prevent "ModuleNotFoundError" in later cells:
# !pip install pvdeg==0.3.3
from pvdeg import letid, collection, utilities, DATA_DIR
import pvdeg
import pvlib
import os
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# This information helps with debugging and getting support :)
import sys
import platform
print("Working on a ", platform.system(), platform.release())
print("Python version ", sys.version)
print("Pandas version ", pd.__version__)
print("pvdeg version ", pvdeg.__version__)
Working on a Linux 6.11.0-1018-azure
Python version 3.11.13 (main, Jun 4 2025, 04:12:12) [GCC 13.3.0]
Pandas version 2.3.3
pvdeg version 0.1.dev1+g51172fdc5
First, we’ll load some data taken from an accelerated test. See Karas et al. 2022 for full details. This data is the average of “Type S” modules from Lab 3. Type S modules were prototype modules made with 48 monocrystalline cells, and degraded about 4-5% in LETID testing. Data throughout testing is shown below:
cell_area = 243 # cm^2
df = pd.read_csv(os.path.join(DATA_DIR, "module test data.csv"))
df["cell Voc"] = df["Voc"] / 48
df["Jsc"] = df["Isc"] / cell_area * 1000
df["% degradation"] = (df["Pmp"] - df["Pmp"].iloc[0]) / df["Pmp"] * 100
df
| Week | Pmp | Isc | Voc | FF | cell Voc | Jsc | % degradation | |
|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 236.7 | 9.91 | 31.86 | 75.01 | 0.663750 | 40.781893 | 0.000000 |
| 1 | 1 | 230.9 | 9.82 | 31.63 | 74.38 | 0.658958 | 40.411523 | -2.511910 |
| 2 | 2 | 228.5 | 9.72 | 31.54 | 74.50 | 0.657083 | 40.000000 | -3.588621 |
| 3 | 3 | 226.9 | 9.70 | 31.56 | 74.10 | 0.657500 | 39.917695 | -4.319083 |
| 4 | 4 | 224.8 | 9.62 | 31.48 | 74.22 | 0.655833 | 39.588477 | -5.293594 |
| 5 | 7 | 235.8 | 9.76 | 31.98 | 75.51 | 0.666250 | 40.164609 | -0.381679 |
The module parameter that is most sensitve to our device input parameters is cell open-circuit voltage, which in this case started at about 0.664 V/cell. We will select reasonable values for solar cell input parameters, and use letid.calc_voc_from_tau() to check if those parameters match the cell Voc of the device we’re trying to model. The important quantities here are bulk lifetime in the initial state (tau_0), wafer thickness, and rear surface recombination velocity.
tau_0 = 120 # [us] reasonable bulk lifetime for commercial-quality p-type silicon, maybe a little on the low side for typical wafer lifetimes, which could range from 100-500 us.
wafer_thickness = 180 # [um] a reasonable wafer thickness for typical commercial silicon solar cells. Wafer thicknesses for Si solar cells are typically 160-180 um.
srv_rear = 100 # [cm/s] a reasonable value for rear surface recombination velocity for passivated emitter and rear cell (PERC) solar cells.
# Typical PERC cells might have a rear SRV anywhere from 50 to 100 cm/s. Higher values for early PERC, lower values for more modern, higher efficiency PERC.
# Other device structures will have different SRV values. E.g., aluminum back surface field (Al-BSF) cells could be ~500 cm/s. TopCON or other high efficiency cell structures will be lower, e.g. 10 cm/s.
# Note that all of these values are intepreted as "lumped" values for the entire rear surface.
isc_0 = df.query("Week == 0")[
"Isc"
].item() # [A] we'll use the short circuit current from the Week 0 test data, instead of trying to calculate it
cell_area = 240.8 # [cm^2] typical cell size for 6-inch pseudosquare monocrystalline silicon wafers
jsc_0 = isc_0 / cell_area * 1000 # [mA/cm^2] short circuit current density
temperature = 25 # [C] standard measurement temperature
voc_0 = letid.calc_voc_from_tau(tau_0, wafer_thickness, srv_rear, jsc_0, temperature)
voc_0
np.float64(0.6611301062313933)
generation_df = pd.read_excel(
os.path.join(DATA_DIR, "PVL_GenProfile.xlsx"), header=0
) # this is an optical generation profile generated by PVLighthouse's OPAL2 default model for 1-sun, normal incident AM1.5 sunlight on a 180-um thick SiNx-coated, pyramid-textured wafer.
generation = generation_df["Generation (cm-3s-1)"]
depth = generation_df["Depth (um)"]
d_base = 27 # cm^2/s electron diffusivity. See https://www2.pvlighthouse.com.au/calculators/mobility%20calculator/mobility%20calculator.aspx for details
Pretty close!
# check to make sure power is close to the measured Week 0 power
ff_0 = df.query("Week == 0")["FF"].item() # [%] fill factor
pmp_0 = (voc_0 * 48) * (jsc_0 * cell_area / 1000) * ff_0 / 100 # [W] maximum power
pmp_0, df.query("Week == 0")["Pmp"].item()
(np.float64(235.89622533600513), 236.7)
Now we do the same thing for the degraded state to determine tau_deg, the bulk lifetime when the module is in its most degraded state. So here the cell Voc target is the roughly 0.656 V measured after 4 weeks of testing.
tau_deg = 80 # [us] degraded bulk lifetime
isc_deg = df.query("Week == 4")[
"Isc"
].item() # [A] we'll use the short circuit current from the Week 4 test data, instead of trying to calculate it
jsc_deg = isc_deg / cell_area * 1000 # [mA/cm^2] short circuit current density
voc_deg = letid.calc_voc_from_tau(
tau_deg, wafer_thickness, srv_rear, jsc_deg, temperature
)
voc_deg
np.float64(0.6538686361228122)
# check to make sure power is close to the measured Week 4 power
ff_deg = df.query("Week == 4")["FF"].item() # [%] fill factor
pmp_deg = (
(voc_deg * 48) * (jsc_deg * cell_area / 1000) * ff_deg / 100
) # [W] maximum power
pmp_deg, df.query("Week == 4")["Pmp"].item()
(np.float64(224.09272908700694), 224.8)
(pmp_0 - pmp_deg) / pmp_0
np.float64(0.050036816961295416)
So for modeling this module, we will use tau_0 = 120 \(\mu s\), tau_deg = 80 \(\mu s\), with wafer_thickness = 180 \(\mu m\) and srv_rear = 100 cm/s.
Great!
The example proceeds below in similar fashion to the outdoor example, using a fixed latitude tilt system at NREL, in Golden, CO, USA, using NSRDB hourly PSM weather data, SAPM temperature models, and module and inverter models from the CEC database.
# load weather and location data, use pvlib read_psm3 function
sam_file = "psm3.csv"
weather, meta = pvdeg.weather.read(
os.path.join(DATA_DIR, sam_file), file_type="PSM3", map_variables=True
)
weather
| Year | Month | Day | Hour | Minute | dni | dhi | ghi | temp_air | dew_point | wind_speed | relative_humidity | poa_global | temp_cell | temp_module | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1999-01-01 00:30:00-07:00 | 1999 | 1 | 1 | 0 | 30 | 0.0 | 0.0 | 0.0 | 0.0 | -5.0 | 1.8 | 79.39 | 0.0 | 0.0 | 0.0 |
| 1999-01-01 01:30:00-07:00 | 1999 | 1 | 1 | 1 | 30 | 0.0 | 0.0 | 0.0 | 0.0 | -4.0 | 1.7 | 80.84 | 0.0 | 0.0 | 0.0 |
| 1999-01-01 02:30:00-07:00 | 1999 | 1 | 1 | 2 | 30 | 0.0 | 0.0 | 0.0 | 0.0 | -4.0 | 1.5 | 82.98 | 0.0 | 0.0 | 0.0 |
| 1999-01-01 03:30:00-07:00 | 1999 | 1 | 1 | 3 | 30 | 0.0 | 0.0 | 0.0 | 0.0 | -4.0 | 1.3 | 85.01 | 0.0 | 0.0 | 0.0 |
| 1999-01-01 04:30:00-07:00 | 1999 | 1 | 1 | 4 | 30 | 0.0 | 0.0 | 0.0 | 0.0 | -4.0 | 1.3 | 85.81 | 0.0 | 0.0 | 0.0 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 1999-12-31 19:30:00-07:00 | 1999 | 12 | 31 | 19 | 30 | 0.0 | 0.0 | 0.0 | 0.0 | -3.0 | 0.9 | 83.63 | 0.0 | 0.0 | 0.0 |
| 1999-12-31 20:30:00-07:00 | 1999 | 12 | 31 | 20 | 30 | 0.0 | 0.0 | 0.0 | 0.0 | -3.0 | 1.2 | 86.82 | 0.0 | 0.0 | 0.0 |
| 1999-12-31 21:30:00-07:00 | 1999 | 12 | 31 | 21 | 30 | 0.0 | 0.0 | 0.0 | 0.0 | -4.0 | 1.6 | 83.78 | 0.0 | 0.0 | 0.0 |
| 1999-12-31 22:30:00-07:00 | 1999 | 12 | 31 | 22 | 30 | 0.0 | 0.0 | 0.0 | 0.0 | -4.0 | 1.7 | 81.22 | 0.0 | 0.0 | 0.0 |
| 1999-12-31 23:30:00-07:00 | 1999 | 12 | 31 | 23 | 30 | 0.0 | 0.0 | 0.0 | 0.0 | -5.0 | 1.8 | 79.43 | 0.0 | 0.0 | 0.0 |
8760 rows × 15 columns
# if our weather file doesn't have precipitable water, calculate it with pvlib
if "precipitable_water" not in weather.columns:
weather["precipitable_water"] = pvlib.atmosphere.gueymard94_pw(
weather["temp_air"], weather["relative_humidity"]
)
# drop unneeded columns
weather = weather[
[
"ghi",
"dni",
"dhi",
"temp_air",
"wind_speed",
"relative_humidity",
"precipitable_water",
]
]
weather
| ghi | dni | dhi | temp_air | wind_speed | relative_humidity | precipitable_water | |
|---|---|---|---|---|---|---|---|
| 1999-01-01 00:30:00-07:00 | 0.0 | 0.0 | 0.0 | 0.0 | 1.8 | 79.39 | 0.891869 |
| 1999-01-01 01:30:00-07:00 | 0.0 | 0.0 | 0.0 | 0.0 | 1.7 | 80.84 | 0.908158 |
| 1999-01-01 02:30:00-07:00 | 0.0 | 0.0 | 0.0 | 0.0 | 1.5 | 82.98 | 0.932199 |
| 1999-01-01 03:30:00-07:00 | 0.0 | 0.0 | 0.0 | 0.0 | 1.3 | 85.01 | 0.955004 |
| 1999-01-01 04:30:00-07:00 | 0.0 | 0.0 | 0.0 | 0.0 | 1.3 | 85.81 | 0.963991 |
| ... | ... | ... | ... | ... | ... | ... | ... |
| 1999-12-31 19:30:00-07:00 | 0.0 | 0.0 | 0.0 | 0.0 | 0.9 | 83.63 | 0.939501 |
| 1999-12-31 20:30:00-07:00 | 0.0 | 0.0 | 0.0 | 0.0 | 1.2 | 86.82 | 0.975338 |
| 1999-12-31 21:30:00-07:00 | 0.0 | 0.0 | 0.0 | 0.0 | 1.6 | 83.78 | 0.941186 |
| 1999-12-31 22:30:00-07:00 | 0.0 | 0.0 | 0.0 | 0.0 | 1.7 | 81.22 | 0.912427 |
| 1999-12-31 23:30:00-07:00 | 0.0 | 0.0 | 0.0 | 0.0 | 1.8 | 79.43 | 0.892318 |
8760 rows × 7 columns
Set up PVlib model#
Note that the module we select here is NOT the same “Type S” module that was tested for LETID. I’m simply trying to find a module in the CEC database with I-V characteristics that are reasonably close to the tested module, so the pvlib calculated DC results are close to how our Type S module might behave in the field.
cec_modules = pvlib.pvsystem.retrieve_sam("CECMod").T
cec_modules[cec_modules["STC"].between(220, 250) & (cec_modules["N_s"] == 48)]
| Technology | Bifacial | STC | PTC | A_c | Length | Width | N_s | I_sc_ref | V_oc_ref | ... | a_ref | I_L_ref | I_o_ref | R_s | R_sh_ref | Adjust | gamma_r | BIPV | Version | Date | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Gintech_Energy_GIN_M6_48_220 | Mono-c-Si | 0 | 220.48 | 194.5 | 1.313 | 1.324 | 0.992 | 48 | 9.31 | 31.3 | ... | 1.521151 | 9.3228 | 0.0 | 0.106087 | 77.164063 | 22.488531 | -0.55 | N | SAM 2018.11.11 r2 | 1/3/2019 |
| Gintech_Energy_GIN_P6_48_220 | Multi-c-Si | 0 | 220.378 | 199.2 | 1.313 | 1.324 | 0.992 | 48 | 9.28 | 31.3 | ... | 1.379815 | 9.379174 | 0.0 | 0.254869 | 374.724518 | 8.824213 | -0.49 | N | SAM 2018.11.11 r2 | 1/3/2019 |
| Gintech_Energy_GIN_M6_48_225 | Mono-c-Si | 0 | 225.844 | 199.1 | 1.313 | 1.324 | 0.992 | 48 | 9.45 | 31.5 | ... | 1.530596 | 9.461989 | 0.0 | 0.100905 | 79.531746 | 22.462965 | -0.55 | N | SAM 2018.11.11 r2 | 1/3/2019 |
| LG_Electronics_Inc__LG230N8K_G4 | Mono-c-Si | 0 | 230.127 | 212.9 | 1.274 | 1.3 | 0.98 | 48 | 9.9 | 30.0 | ... | 1.110894 | 10.312051 | 0.0 | 0.307502 | 314.551514 | 2.112491 | -0.38 | N | SAM 2018.11.11 r2 | 1/3/2019 |
| LG_Electronics_Inc__LG235N8K_G4 | Mono-c-Si | 0 | 235.216 | 217.6 | 1.274 | 1.3 | 0.98 | 48 | 9.96 | 30.2 | ... | 1.124688 | 10.375943 | 0.0 | 0.278936 | 250.799469 | 3.374386 | -0.38 | N | SAM 2018.11.11 r2 | 1/3/2019 |
| LG_Electronics_Inc__LG240N8K_G4 | Mono-c-Si | 0 | 240.1 | 222.4 | 1.274 | 1.3 | 0.98 | 48 | 10.01 | 30.5 | ... | 1.134983 | 10.313996 | 0.0 | 0.263453 | 3976.513916 | 3.244429 | -0.38 | N | SAM 2018.11.11 r2 | 1/3/2019 |
| LG_Electronics_Inc__LG245N8K_G4 | Mono-c-Si | 0 | 245.016 | 227.1 | 1.274 | 1.3 | 0.98 | 48 | 10.06 | 30.8 | ... | 1.150454 | 10.36712 | 0.0 | 0.246041 | 1112.830811 | 4.077489 | -0.38 | N | SAM 2018.11.11 r2 | 1/3/2019 |
| Prism_Solar_Technologies_Bi48_279BSTC | Mono-c-Si | 1 | 220.472 | 199.3 | 1.668 | 1.695 | 0.984 | 48 | 9.15 | 31.0 | ... | 1.266369 | 9.15029 | 0.0 | 0.210912 | 6628.005371 | 13.999823 | -0.4399 | N | SAM 2018.11.11 r2 | 1/3/2019 |
| Prism_Solar_Technologies_Bi48_286BSTC | Mono-c-Si | 1 | 225.298 | 204.0 | 1.668 | 1.695 | 0.984 | 48 | 9.35 | 31.0 | ... | 1.266347 | 9.350275 | 0.0 | 0.206403 | 7016.816406 | 13.996228 | -0.4399 | N | SAM 2018.11.11 r2 | 1/3/2019 |
9 rows × 25 columns
The LG ones look close to the module we’re trying to model. Pmp around 235W, Isc around 9.9A. Let’s go with ‘LG_Electronics_Inc__LG235N8K_G4’
cec_modules = cec_modules.T
cec_module = cec_modules["LG_Electronics_Inc__LG235N8K_G4"]
# import the rest of the pvlib stuff
# we'll use the SAPM temperature model open-rack glass/polymer coeffecients.
from pvlib.temperature import TEMPERATURE_MODEL_PARAMETERS
from pvlib.location import Location
from pvlib.pvsystem import PVSystem
from pvlib.modelchain import ModelChain
cec_inverters = pvlib.pvsystem.retrieve_sam("cecinverter")
cec_inverter = cec_inverters["ABB__ULTRA_750_TL_OUTD_1_US_690_x_y_z__690V_"]
temperature_model_parameters = TEMPERATURE_MODEL_PARAMETERS["sapm"][
"open_rack_glass_polymer"
]
# set up system in pvlib
lat = meta["latitude"]
lon = meta["longitude"]
tz = meta["tz"]
elevation = meta["altitude"]
surface_tilt = lat # fixed, latitude tilt
surface_azimuth = 180 # south-facing
location = Location(lat, lon, tz, elevation, "Golden, CO, USA")
system = PVSystem(
surface_tilt=surface_tilt,
surface_azimuth=surface_azimuth,
module_parameters=cec_module,
inverter_parameters=cec_inverter,
temperature_model_parameters=temperature_model_parameters,
)
# create and run pvlib modelchain
mc = ModelChain(system, location, aoi_model="physical")
mc.run_model(weather)
ModelChain:
name: None
clearsky_model: ineichen
transposition_model: haydavies
solar_position_method: nrel_numpy
airmass_model: kastenyoung1989
dc_model: cec
ac_model: sandia_inverter
aoi_model: physical_aoi_loss
spectral_model: no_spectral_loss
temperature_model: sapm_temp
losses_model: no_extra_losses
Set up timeseries#
In this example, injection is a function of both the operating point of the module (which we will assume is maximum power point) and irradiance. Maximum power point injection is equivalent to \((I_{sc}-I_{mp})/I_{sc}\times Ee\), where \(Ee\) is effective irradiance, the irradiance absorbed by the module’s cells. We normalize it to 1-sun irradiance, 1000 \(W/m^2\).
We will use the irradiance, DC operating point, and cell temperature from the pvlib modelchain results.
ee = mc.results.effective_irradiance
# injection = (mc.results.dc['i_sc']-mc.results.dc['i_mp'])/(mc.results.dc['i_sc'])*(ee/1000)
injection = letid.calc_injection_outdoors(mc.results)
temperature = mc.results.cell_temperature
timesteps = pd.DataFrame(
{"Temperature": temperature, "Injection": injection}
) # create a DataFrame with cell temperature and injection
timesteps.reset_index(
inplace=True
) # reset the index so datetime is a column. I prefer integer indexing.
timesteps.rename(columns={"index": "Datetime"}, inplace=True)
Remaining degradation parameters:#
We’ve already set our important device parameters: tau_0, tau_deg, wafer_thickness, srv_rear, cell_area, etc, but we need a few more: generation profile and carrier diffusivity. These are necessary for calculating current collection, and the “default” values provided here should be sufficient for most use cases.
The rest of the quantities to define are: the initial percentage of defects in each state (A, B, and C), and the dictionary of mechanism parameters.
In this example, we’ll assume the device starts in the fully-undegraded state (100% state A), and we’ll use the parameters for LETID degradation from Repins.
generation_df = pd.read_excel(
os.path.join(DATA_DIR, "PVL_GenProfile.xlsx"), header=0
) # this is an optical generation profile generated by PVLighthouse's OPAL2 default model for 1-sun, normal incident AM1.5 sunlight on a 180-um thick SiNx-coated, pyramid-textured wafer.
generation = generation_df["Generation (cm-3s-1)"]
depth = generation_df["Depth (um)"]
d_base = 27 # cm^2/s electron diffusivity. See https://www2.pvlighthouse.com.au/calculators/mobility%20calculator/mobility%20calculator.aspx for details
# starting defect state percentages
nA_0 = 100
nB_0 = 0
nC_0 = 0
mechanism_params = utilities.get_kinetics("repins")
timesteps[["NA", "NB", "NC", "tau"]] = (
np.nan
) # create columns for defect state percentages and lifetime, fill with NaNs for now, to fill iteratively below
timesteps.loc[0, ["NA", "NB", "NC"]] = (
nA_0,
nB_0,
nC_0,
) # assign first timestep defect state percentages
timesteps.loc[0, "tau"] = letid.tau_now(
tau_0, tau_deg, nB_0
) # calculate tau for the first timestep
timesteps
| Datetime | Temperature | Injection | NA | NB | NC | tau | |
|---|---|---|---|---|---|---|---|
| 0 | 1999-01-01 00:30:00-07:00 | 0.0 | NaN | 100.0 | 0.0 | 0.0 | 120.0 |
| 1 | 1999-01-01 01:30:00-07:00 | 0.0 | NaN | NaN | NaN | NaN | NaN |
| 2 | 1999-01-01 02:30:00-07:00 | 0.0 | NaN | NaN | NaN | NaN | NaN |
| 3 | 1999-01-01 03:30:00-07:00 | 0.0 | NaN | NaN | NaN | NaN | NaN |
| 4 | 1999-01-01 04:30:00-07:00 | 0.0 | NaN | NaN | NaN | NaN | NaN |
| ... | ... | ... | ... | ... | ... | ... | ... |
| 8755 | 1999-12-31 19:30:00-07:00 | 0.0 | NaN | NaN | NaN | NaN | NaN |
| 8756 | 1999-12-31 20:30:00-07:00 | 0.0 | NaN | NaN | NaN | NaN | NaN |
| 8757 | 1999-12-31 21:30:00-07:00 | 0.0 | NaN | NaN | NaN | NaN | NaN |
| 8758 | 1999-12-31 22:30:00-07:00 | 0.0 | NaN | NaN | NaN | NaN | NaN |
| 8759 | 1999-12-31 23:30:00-07:00 | 0.0 | NaN | NaN | NaN | NaN | NaN |
8760 rows × 7 columns
Run through timesteps#
Since each timestep depends on the preceding timestep, we need to calculate in a loop. This will take a few minutes depending on the length of the timeseries.
for index, timestep in timesteps.iterrows():
# first row tau has already been assigned
if index == 0:
pass
# loop through rows, new tau calculated based on previous NB. Reaction proceeds based on new tau.
else:
n_A = timesteps.at[index - 1, "NA"]
n_B = timesteps.at[index - 1, "NB"]
n_C = timesteps.at[index - 1, "NC"]
tau = letid.tau_now(tau_0, tau_deg, n_B)
jsc = collection.calculate_jsc_from_tau_cp(
tau, wafer_thickness, d_base, srv_rear, generation, depth
)
temperature = timesteps.at[index, "Temperature"]
injection = timesteps.at[index, "Injection"]
# calculate defect reaction kinetics: reaction constant and carrier concentration factor.
k_AB = letid.k_ij(
mechanism_params["v_ab"], mechanism_params["ea_ab"], temperature
)
k_BA = letid.k_ij(
mechanism_params["v_ba"], mechanism_params["ea_ba"], temperature
)
k_BC = letid.k_ij(
mechanism_params["v_bc"], mechanism_params["ea_bc"], temperature
)
k_CB = letid.k_ij(
mechanism_params["v_cb"], mechanism_params["ea_cb"], temperature
)
x_ab = letid.carrier_factor(
tau,
"ab",
temperature,
injection,
jsc,
wafer_thickness,
srv_rear,
mechanism_params,
)
x_ba = letid.carrier_factor(
tau,
"ba",
temperature,
injection,
jsc,
wafer_thickness,
srv_rear,
mechanism_params,
)
x_bc = letid.carrier_factor(
tau,
"bc",
temperature,
injection,
jsc,
wafer_thickness,
srv_rear,
mechanism_params,
)
# calculate the instantaneous change in NA, NB, and NC
dN_Adt = (k_BA * n_B * x_ba) - (k_AB * n_A * x_ab)
dN_Bdt = (
(k_AB * n_A * x_ab) + (k_CB * n_C) - ((k_BA * x_ba + k_BC * x_bc) * n_B)
)
dN_Cdt = (k_BC * n_B * x_bc) - (k_CB * n_C)
t_step = (
timesteps.at[index, "Datetime"] - timesteps.at[index - 1, "Datetime"]
).total_seconds()
# assign new defect state percentages
timesteps.at[index, "NA"] = n_A + dN_Adt * t_step
timesteps.at[index, "NB"] = n_B + dN_Bdt * t_step
timesteps.at[index, "NC"] = n_C + dN_Cdt * t_step
timesteps["tau"] = letid.tau_now(tau_0, tau_deg, timesteps["NB"])
# calculate device Jsc for every timestep. Unfortunately this requires an integration so I think we have to run through a loop. Device Jsc allows calculation of device Voc.
for index, timestep in timesteps.iterrows():
jsc_now = collection.calculate_jsc_from_tau_cp(
timesteps.at[index, "tau"], wafer_thickness, d_base, srv_rear, generation, depth
)
timesteps.at[index, "Jsc"] = jsc_now
timesteps.at[index, "Voc"] = letid.calc_voc_from_tau(
timesteps.at[index, "tau"], wafer_thickness, srv_rear, jsc_now, temperature=25
)
timesteps = letid.calc_device_params(
timesteps, cell_area
) # this function quickly calculates the rest of the device parameters: Isc, FF, max power, and normalized max power
timesteps
| Datetime | Temperature | Injection | NA | NB | NC | tau | Jsc | Voc | Isc | FF | Pmp | Pmp_norm | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1999-01-01 00:30:00-07:00 | 0.0 | NaN | 100.000000 | 0.000000e+00 | 0.000000e+00 | 120.000000 | 41.451328 | 0.661315 | 9.981480 | 0.840101 | 5.545424 | 1.000000 |
| 1 | 1999-01-01 01:30:00-07:00 | 0.0 | NaN | 100.000000 | 1.683090e-15 | 0.000000e+00 | 120.000000 | 41.451328 | 0.661315 | 9.981480 | 0.840101 | 5.545424 | 1.000000 |
| 2 | 1999-01-01 02:30:00-07:00 | 0.0 | NaN | 100.000000 | 3.366181e-15 | 5.269266e-36 | 120.000000 | 41.451328 | 0.661315 | 9.981480 | 0.840101 | 5.545424 | 1.000000 |
| 3 | 1999-01-01 03:30:00-07:00 | 0.0 | NaN | 100.000000 | 5.049271e-15 | 1.580780e-35 | 120.000000 | 41.451328 | 0.661315 | 9.981480 | 0.840101 | 5.545424 | 1.000000 |
| 4 | 1999-01-01 04:30:00-07:00 | 0.0 | NaN | 100.000000 | 6.732362e-15 | 3.161560e-35 | 120.000000 | 41.451328 | 0.661315 | 9.981480 | 0.840101 | 5.545424 | 1.000000 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 8755 | 1999-12-31 19:30:00-07:00 | 0.0 | NaN | 29.749662 | 6.666236e+01 | 3.587983e+00 | 90.001455 | 41.342623 | 0.656723 | 9.955304 | 0.839281 | 5.487117 | 0.989486 |
| 8756 | 1999-12-31 20:30:00-07:00 | 0.0 | NaN | 29.749662 | 6.666236e+01 | 3.587983e+00 | 90.001455 | 41.342623 | 0.656723 | 9.955304 | 0.839281 | 5.487117 | 0.989486 |
| 8757 | 1999-12-31 21:30:00-07:00 | 0.0 | NaN | 29.749662 | 6.666236e+01 | 3.587983e+00 | 90.001455 | 41.342623 | 0.656723 | 9.955304 | 0.839281 | 5.487117 | 0.989486 |
| 8758 | 1999-12-31 22:30:00-07:00 | 0.0 | NaN | 29.749662 | 6.666236e+01 | 3.587983e+00 | 90.001455 | 41.342623 | 0.656723 | 9.955304 | 0.839281 | 5.487117 | 0.989486 |
| 8759 | 1999-12-31 23:30:00-07:00 | 0.0 | NaN | 29.749662 | 6.666236e+01 | 3.587983e+00 | 90.001455 | 41.342623 | 0.656723 | 9.955304 | 0.839281 | 5.487117 | 0.989486 |
8760 rows × 13 columns
Note of course that all these calculated device parameters are modeled STC device parameters, not the instantaneous, weather-dependent values. We’ll merge back in the pvlib results for convenience, but these don’t reflect the device degradation. We’ll calculate energy loss next
timesteps = timesteps.merge(mc.results.dc, left_on="Datetime", right_index=True)
timesteps = timesteps.merge(
pd.DataFrame(mc.results.effective_irradiance, columns=["Effective irradiance"]),
left_on="Datetime",
right_index=True,
)
timesteps = timesteps.merge(mc.results.weather, left_on="Datetime", right_index=True)
timesteps
| Datetime | Temperature | Injection | NA | NB | NC | tau | Jsc | Voc | Isc | ... | p_mp | i_x | i_xx | Effective irradiance | ghi | dhi | dni | wind_speed | temp_air | precipitable_water | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1999-01-01 00:30:00-07:00 | 0.0 | NaN | 100.000000 | 0.000000e+00 | 0.000000e+00 | 120.000000 | 41.451328 | 0.661315 | 9.981480 | ... | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.8 | 0.0 | 0.891869 |
| 1 | 1999-01-01 01:30:00-07:00 | 0.0 | NaN | 100.000000 | 1.683090e-15 | 0.000000e+00 | 120.000000 | 41.451328 | 0.661315 | 9.981480 | ... | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.7 | 0.0 | 0.908158 |
| 2 | 1999-01-01 02:30:00-07:00 | 0.0 | NaN | 100.000000 | 3.366181e-15 | 5.269266e-36 | 120.000000 | 41.451328 | 0.661315 | 9.981480 | ... | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.5 | 0.0 | 0.932199 |
| 3 | 1999-01-01 03:30:00-07:00 | 0.0 | NaN | 100.000000 | 5.049271e-15 | 1.580780e-35 | 120.000000 | 41.451328 | 0.661315 | 9.981480 | ... | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.3 | 0.0 | 0.955004 |
| 4 | 1999-01-01 04:30:00-07:00 | 0.0 | NaN | 100.000000 | 6.732362e-15 | 3.161560e-35 | 120.000000 | 41.451328 | 0.661315 | 9.981480 | ... | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.3 | 0.0 | 0.963991 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 8755 | 1999-12-31 19:30:00-07:00 | 0.0 | NaN | 29.749662 | 6.666236e+01 | 3.587983e+00 | 90.001455 | 41.342623 | 0.656723 | 9.955304 | ... | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.9 | 0.0 | 0.939501 |
| 8756 | 1999-12-31 20:30:00-07:00 | 0.0 | NaN | 29.749662 | 6.666236e+01 | 3.587983e+00 | 90.001455 | 41.342623 | 0.656723 | 9.955304 | ... | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.2 | 0.0 | 0.975338 |
| 8757 | 1999-12-31 21:30:00-07:00 | 0.0 | NaN | 29.749662 | 6.666236e+01 | 3.587983e+00 | 90.001455 | 41.342623 | 0.656723 | 9.955304 | ... | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.6 | 0.0 | 0.941186 |
| 8758 | 1999-12-31 22:30:00-07:00 | 0.0 | NaN | 29.749662 | 6.666236e+01 | 3.587983e+00 | 90.001455 | 41.342623 | 0.656723 | 9.955304 | ... | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.7 | 0.0 | 0.912427 |
| 8759 | 1999-12-31 23:30:00-07:00 | 0.0 | NaN | 29.749662 | 6.666236e+01 | 3.587983e+00 | 90.001455 | 41.342623 | 0.656723 | 9.955304 | ... | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.8 | 0.0 | 0.892318 |
8760 rows × 27 columns
Plot the results#
from cycler import cycler
plt.style.use("default")
fig, ax = plt.subplots()
ax.set_prop_cycle(
cycler("color", ["tab:blue", "tab:orange", "tab:green"])
+ cycler("linestyle", ["-", "--", "-."])
)
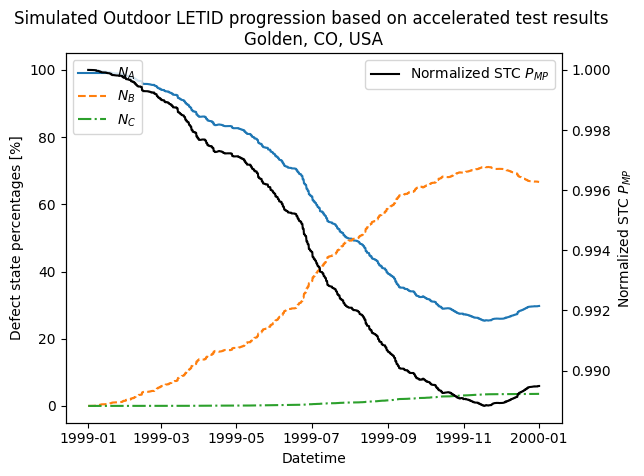
ax.plot(timesteps["Datetime"], timesteps[["NA", "NB", "NC"]].values)
ax.legend(labels=["$N_A$", "$N_B$", "$N_C$"], loc="upper left")
ax.set_ylabel("Defect state percentages [%]")
ax.set_xlabel("Datetime")
ax2 = ax.twinx()
ax2.plot(
timesteps["Datetime"],
timesteps["Pmp_norm"],
c="black",
label="Normalized STC $P_{MP}$",
)
ax2.legend(loc="upper right")
ax2.set_ylabel("Normalized STC $P_{MP}$")
ax.set_title(
"Simulated Outdoor LETID progression based on accelerated test results \n"
f"{location.name}"
)
plt.show()
import matplotlib.dates as mdates
plt.style.use("default")
fig, ax = plt.subplots()
ax.plot(
timesteps["Datetime"],
timesteps["Pmp_norm"],
c="black",
label="Normalized STC $P_{MP}$",
)
ax.plot(timesteps["Datetime"], np.ones(len(timesteps)), c="black")
ax.fill_between(
timesteps["Datetime"],
np.ones(len(timesteps)),
timesteps["Pmp_norm"],
color="grey",
alpha=0.5,
)
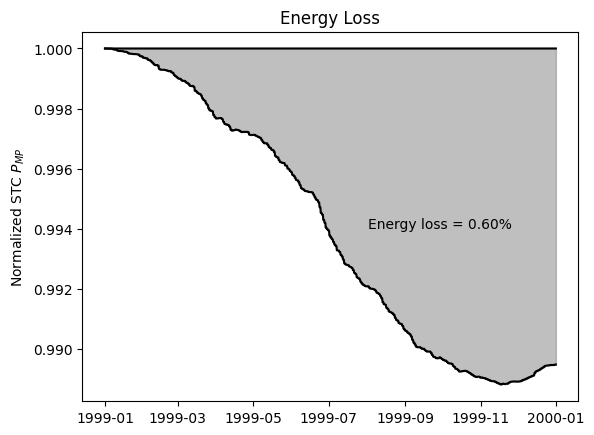
ax.set_ylabel("Normalized STC $P_{MP}$")
ax.set_title("Energy Loss")
loss = letid.calc_energy_loss(timesteps)
ax.text(mdates.datestr2num("1999-08-02"), 0.994, s=f"Energy loss = {loss * 100:.2f}%")
plt.show()
Index(['Datetime', 'Temperature', 'Injection', 'NA', 'NB', 'NC', 'tau', 'Jsc',
'Voc', 'Isc', 'FF', 'Pmp', 'Pmp_norm', 'i_sc', 'v_oc', 'i_mp', 'v_mp',
'p_mp', 'i_x', 'i_xx', 'Effective irradiance', 'ghi', 'dhi', 'dni',
'wind_speed', 'temp_air', 'precipitable_water'],
dtype='object')
import matplotlib.dates as mdates
from scipy.integrate import cumulative_trapezoid, simpson
fig, axs = plt.subplots(3, 1, figsize=(10, 10), sharex=True)
ax1, ax2, ax3 = axs
ax1.plot(timesteps["Datetime"], timesteps["p_mp"], label="Base $P_{MP}$")
ax1.plot(
timesteps["Datetime"],
timesteps["p_mp"] * timesteps["Pmp_norm"],
label="Degraded $P_{MP}$",
alpha=0.7,
)
ax1.legend(loc="lower left")
axin1 = ax1.inset_axes([0.55, 0.25, 0.43, 0.43])
axin1.plot(timesteps["Datetime"], timesteps["p_mp"])
axin1.plot(timesteps["Datetime"], timesteps["p_mp"] * timesteps["Pmp_norm"], alpha=0.7)
axin1.set_xlim(mdates.datestr2num("1999-12-04"), mdates.datestr2num("1999-12-11"))
axin1.set_ylim(50, 240)
axin1.tick_params(axis="x", labelrotation=15)
ax1.indicate_inset_zoom(axin1)
start = timesteps["Datetime"].iloc[0]
timesteps["Timedelta"] = [
(d - start).total_seconds() / 3600 for d in timesteps["Datetime"]
]
ax2.plot(
timesteps["Datetime"],
cumulative_trapezoid(timesteps["p_mp"] / 1000, timesteps["Timedelta"], initial=0),
label="Cumulative energy, base",
)
ax2.plot(
timesteps["Datetime"],
cumulative_trapezoid(
(timesteps["p_mp"] * timesteps["Pmp_norm"]) / 1000,
timesteps["Timedelta"],
initial=0,
),
label="Cumulative energy, degraded",
)
ax2.fill_between(
timesteps["Datetime"],
(cumulative_trapezoid(timesteps["p_mp"], timesteps["Timedelta"], initial=0) / 1000),
(
cumulative_trapezoid(
timesteps["p_mp"] * timesteps["Pmp_norm"], timesteps["Timedelta"], initial=0
)
/ 1000
),
alpha=0.5,
color="C1",
label="Energy loss",
)
ax2.legend()
axin2 = ax2.inset_axes([0.55, 0.25, 0.43, 0.43])
axin2.plot(
timesteps["Datetime"],
cumulative_trapezoid(timesteps["p_mp"] / 1000, timesteps["Timedelta"], initial=0),
)
axin2.plot(
timesteps["Datetime"],
cumulative_trapezoid(
(timesteps["p_mp"] * timesteps["Pmp_norm"]) / 1000,
timesteps["Timedelta"],
initial=0,
),
)
axin2.fill_between(
timesteps["Datetime"],
(cumulative_trapezoid(timesteps["p_mp"], timesteps["Timedelta"], initial=0) / 1000),
(
cumulative_trapezoid(
timesteps["p_mp"] * timesteps["Pmp_norm"], timesteps["Timedelta"], initial=0
)
/ 1000
),
alpha=0.5,
color="C1",
)
axin2.set_xlim(mdates.datestr2num("1999-12-04"), mdates.datestr2num("1999-12-11"))
axin2.set_ylim(412, 427)
axin2.tick_params(axis="x", labelrotation=15)
ax2.indicate_inset_zoom(axin2)
ax3.set_xlabel("Datetime")
ax3.plot(
timesteps["Datetime"],
(cumulative_trapezoid(timesteps["p_mp"], timesteps["Timedelta"], initial=0) / 1000)
- (
cumulative_trapezoid(
timesteps["p_mp"] * timesteps["Pmp_norm"], timesteps["Timedelta"], initial=0
)
/ 1000
),
label="Cumulative energy loss",
)
ax3.legend()
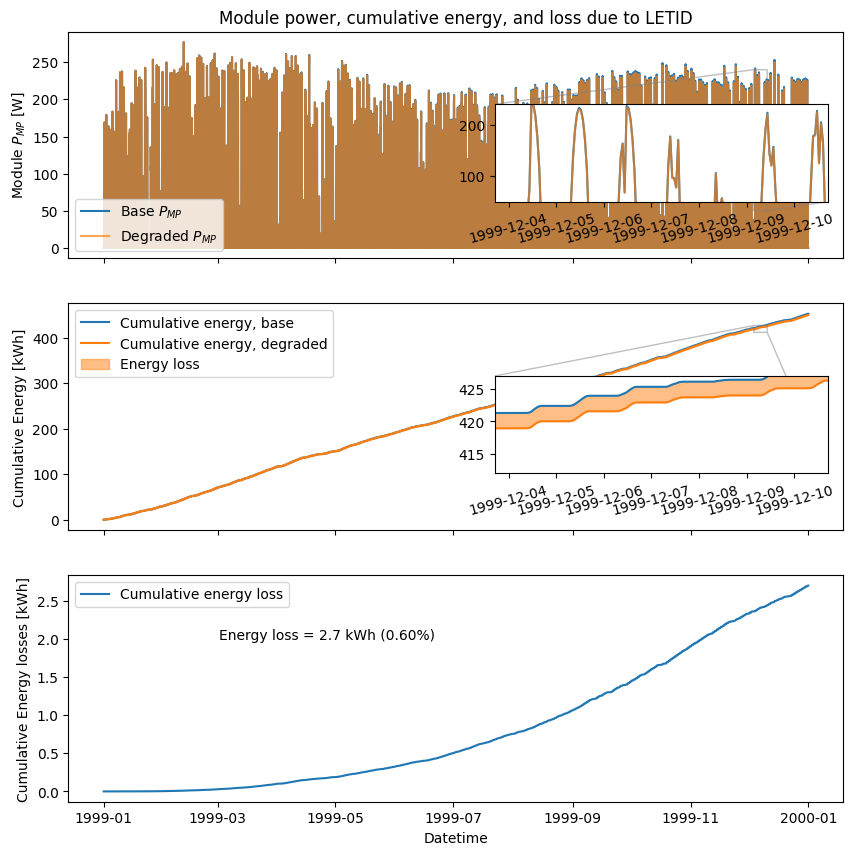
loss = letid.calc_energy_loss(timesteps)
energy = simpson(timesteps["p_mp"] / 1000, timesteps["Timedelta"])
ax3.text(
mdates.datestr2num("1999-03-02"),
2,
s=f"Energy loss = {loss * energy:.1f} kWh ({loss * 100:.2f}%)",
)
ax1.set_ylabel("Module $P_{MP}$ [W]")
ax2.set_ylabel("Cumulative Energy [kWh]")
ax3.set_ylabel("Cumulative Energy losses [kWh]")
ax1.set_title("Module power, cumulative energy, and loss due to LETID")
plt.show()
Index(['Datetime', 'Temperature', 'Injection', 'NA', 'NB', 'NC', 'tau', 'Jsc',
'Voc', 'Isc', 'FF', 'Pmp', 'Pmp_norm', 'i_sc', 'v_oc', 'i_mp', 'v_mp',
'p_mp', 'i_x', 'i_xx', 'Effective irradiance', 'ghi', 'dhi', 'dni',
'wind_speed', 'temp_air', 'precipitable_water', 'Timedelta'],
dtype='object')
The function calc_letid_outdoors wraps all of the steps above into a single function:#
mechanism_params = "repins"
letid.calc_letid_outdoors(
tau_0,
tau_deg,
wafer_thickness,
srv_rear,
nA_0,
nB_0,
nC_0,
weather,
meta,
mechanism_params,
generation_df,
module_parameters=cec_module,
)
| Temperature | Injection | NA | NB | NC | tau | Jsc | Voc | Isc | FF | Pmp | Pmp_norm | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| time | ||||||||||||
| 1999-01-01 00:30:00-07:00 | 0.0 | NaN | 100.000000 | 0.000000e+00 | 0.000000e+00 | 120.000000 | 41.451328 | 0.661315 | 10.072673 | 0.840101 | 5.596088 | 1.000000 |
| 1999-01-01 01:30:00-07:00 | 0.0 | NaN | 100.000000 | 1.683090e-15 | 0.000000e+00 | 120.000000 | 41.451328 | 0.661315 | 10.072673 | 0.840101 | 5.596088 | 1.000000 |
| 1999-01-01 02:30:00-07:00 | 0.0 | NaN | 100.000000 | 3.366181e-15 | 5.269266e-36 | 120.000000 | 41.451328 | 0.661315 | 10.072673 | 0.840101 | 5.596088 | 1.000000 |
| 1999-01-01 03:30:00-07:00 | 0.0 | NaN | 100.000000 | 5.049271e-15 | 1.580780e-35 | 120.000000 | 41.451328 | 0.661315 | 10.072673 | 0.840101 | 5.596088 | 1.000000 |
| 1999-01-01 04:30:00-07:00 | 0.0 | NaN | 100.000000 | 6.732362e-15 | 3.161560e-35 | 120.000000 | 41.451328 | 0.661315 | 10.072673 | 0.840101 | 5.596088 | 1.000000 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 1999-12-31 19:30:00-07:00 | 0.0 | NaN | 29.749662 | 6.666236e+01 | 3.587983e+00 | 90.001455 | 41.342623 | 0.656723 | 10.046257 | 0.839281 | 5.537249 | 0.989486 |
| 1999-12-31 20:30:00-07:00 | 0.0 | NaN | 29.749662 | 6.666236e+01 | 3.587983e+00 | 90.001455 | 41.342623 | 0.656723 | 10.046257 | 0.839281 | 5.537249 | 0.989486 |
| 1999-12-31 21:30:00-07:00 | 0.0 | NaN | 29.749662 | 6.666236e+01 | 3.587983e+00 | 90.001455 | 41.342623 | 0.656723 | 10.046257 | 0.839281 | 5.537249 | 0.989486 |
| 1999-12-31 22:30:00-07:00 | 0.0 | NaN | 29.749662 | 6.666236e+01 | 3.587983e+00 | 90.001455 | 41.342623 | 0.656723 | 10.046257 | 0.839281 | 5.537249 | 0.989486 |
| 1999-12-31 23:30:00-07:00 | 0.0 | NaN | 29.749662 | 6.666236e+01 | 3.587983e+00 | 90.001455 | 41.342623 | 0.656723 | 10.046257 | 0.839281 | 5.537249 | 0.989486 |
8760 rows × 12 columns
timesteps
| Datetime | Temperature | Injection | NA | NB | NC | tau | Jsc | Voc | Isc | ... | i_x | i_xx | Effective irradiance | ghi | dhi | dni | wind_speed | temp_air | precipitable_water | Timedelta | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1999-01-01 00:30:00-07:00 | 0.0 | NaN | 100.000000 | 0.000000e+00 | 0.000000e+00 | 120.000000 | 41.451328 | 0.661315 | 9.981480 | ... | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.8 | 0.0 | 0.891869 | 0.0 |
| 1 | 1999-01-01 01:30:00-07:00 | 0.0 | NaN | 100.000000 | 1.683090e-15 | 0.000000e+00 | 120.000000 | 41.451328 | 0.661315 | 9.981480 | ... | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.7 | 0.0 | 0.908158 | 1.0 |
| 2 | 1999-01-01 02:30:00-07:00 | 0.0 | NaN | 100.000000 | 3.366181e-15 | 5.269266e-36 | 120.000000 | 41.451328 | 0.661315 | 9.981480 | ... | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.5 | 0.0 | 0.932199 | 2.0 |
| 3 | 1999-01-01 03:30:00-07:00 | 0.0 | NaN | 100.000000 | 5.049271e-15 | 1.580780e-35 | 120.000000 | 41.451328 | 0.661315 | 9.981480 | ... | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.3 | 0.0 | 0.955004 | 3.0 |
| 4 | 1999-01-01 04:30:00-07:00 | 0.0 | NaN | 100.000000 | 6.732362e-15 | 3.161560e-35 | 120.000000 | 41.451328 | 0.661315 | 9.981480 | ... | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.3 | 0.0 | 0.963991 | 4.0 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 8755 | 1999-12-31 19:30:00-07:00 | 0.0 | NaN | 29.749662 | 6.666236e+01 | 3.587983e+00 | 90.001455 | 41.342623 | 0.656723 | 9.955304 | ... | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.9 | 0.0 | 0.939501 | 8755.0 |
| 8756 | 1999-12-31 20:30:00-07:00 | 0.0 | NaN | 29.749662 | 6.666236e+01 | 3.587983e+00 | 90.001455 | 41.342623 | 0.656723 | 9.955304 | ... | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.2 | 0.0 | 0.975338 | 8756.0 |
| 8757 | 1999-12-31 21:30:00-07:00 | 0.0 | NaN | 29.749662 | 6.666236e+01 | 3.587983e+00 | 90.001455 | 41.342623 | 0.656723 | 9.955304 | ... | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.6 | 0.0 | 0.941186 | 8757.0 |
| 8758 | 1999-12-31 22:30:00-07:00 | 0.0 | NaN | 29.749662 | 6.666236e+01 | 3.587983e+00 | 90.001455 | 41.342623 | 0.656723 | 9.955304 | ... | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.7 | 0.0 | 0.912427 | 8758.0 |
| 8759 | 1999-12-31 23:30:00-07:00 | 0.0 | NaN | 29.749662 | 6.666236e+01 | 3.587983e+00 | 90.001455 | 41.342623 | 0.656723 | 9.955304 | ... | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.8 | 0.0 | 0.892318 | 8759.0 |
8760 rows × 28 columns
