Postprocess

Perform early prediction

python applications/early_prediction.py -df bird/postprocess/data_early

Generates

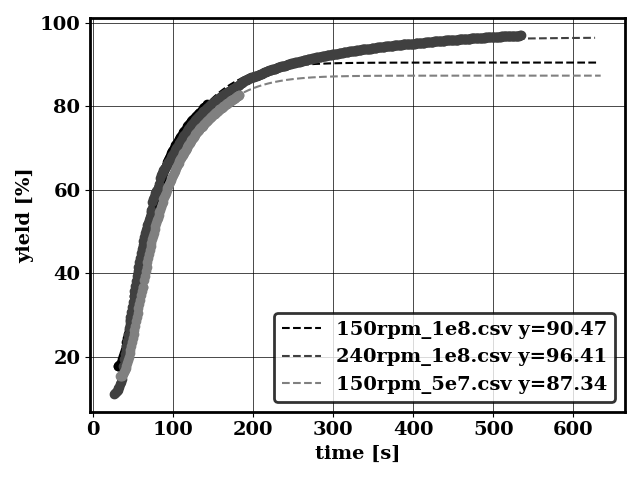
Determinisitc early prediction
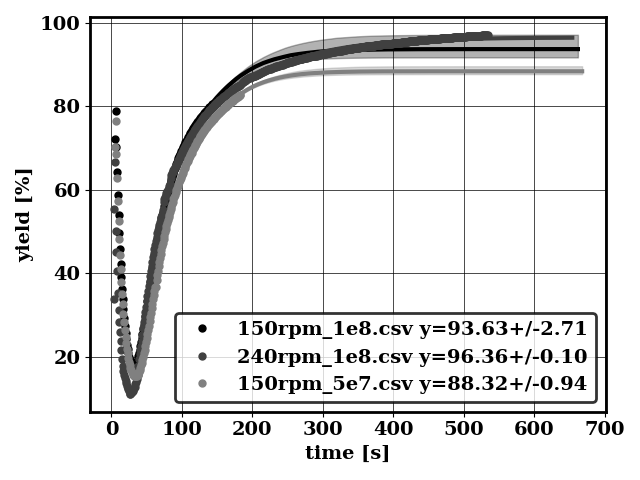
Uncertainty-aware early prediction

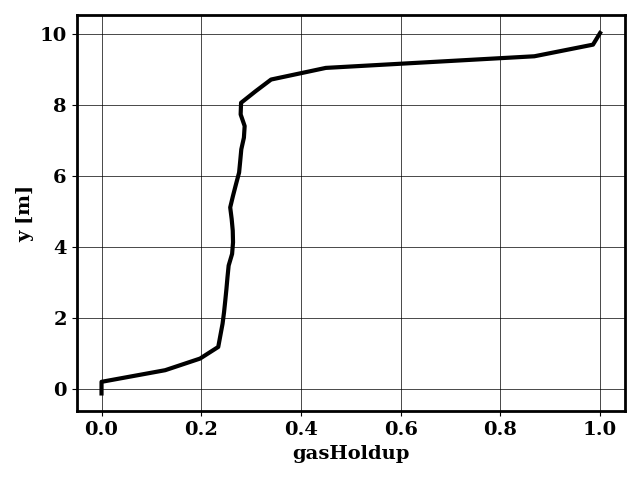
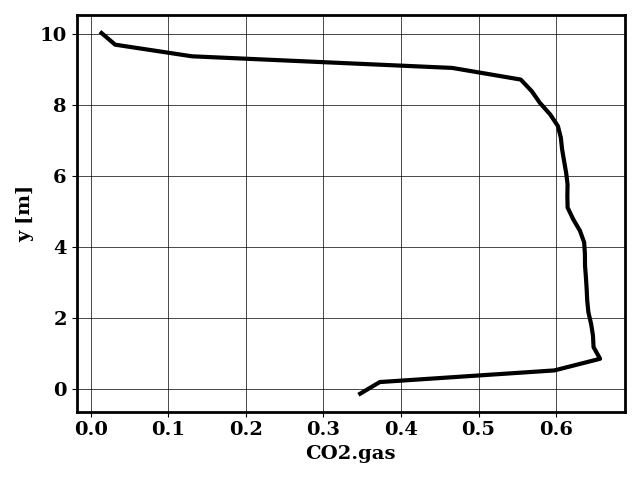
Plot conditional means

python applications/compute_conditional_mean.py -f bird/postprocess/data_conditional_mean -avg 2

Generates (among others)

Height-conditional gas holdup
Height-conditional CO2 gas fraction

Compute kLa with uncertainty estimates

Based on the time-history of the concentration of a species, one can calculate kLa by fitting the function

\[(C^* - C_0) (1-\exp(-kLa (t-t_0)) + C_0\]

where \(C^*\) is the equilibrium concentration (to be fitted), \(C_0\) is the initial concentration, \(t\) is time, \(t_0\) is the initial time after which concentration is recorded

Accurate estimates can be obtained if sufficient data is acquired. Otherwise, it may be useful to derive uncertainty estimates about \(C^*\) and \(kLa\) (the parameters fitted)

This can be achieved with a Bayesian calibration procedure. The calibration is conducted by removing transient data, and by doing a data bootstrapping. The number of data to remove in the transient phase is automatically determined by examining how accurate is the fit.

python applications/compute_kla_uq.py -i bird/postprocess/data_kla/volume_avg.dat -ti 0 -ci 1 -mc 10

Generates

Chopping index = 0
Chopping index = 1
Chopping index = 2
Chopping index = 3
Chopping index = 4
Doing data bootstrapping
      scenario 0
      scenario 1
      scenario 2
      scenario 3
For bird/postprocess/data_kla/volume_avg.dat with time index: 0, concentration index: 1
     kla = 0.09005 +/- 0.0006387
     cstar = 0.3107 +/- 0.0006122
Without data bootstrap
     kla = 0.09014 +/- 0.0005957
     cstar = 0.3105 +/- 0.0005472