Traveling Salesperson Problem (TSP) Environment

The TSP is a classical, NP-hard combinatorial optimization problem that admits a graph search formulation. The application of RL for solving large-scale TSP problems is an active research area, and we do not claim to provide state-of-the-art RL solutions as part of this library. Instead, we demonstrate how to implement the TSP as a graphenv so that researchers interested in RL-based solutions can leverage RLLib as a scalable framework upon which their custom algorithms can be implemented and trained.

Problem statement

In the version of the TSP we consider, one is given \(N\) nodes (cities) in the unit square, and \(N(N-1)/2\) (\(N\) choose \(2\)) edges (highways) that connect each pair of nodes. Each edge is weighted by the Euclidean distance between its endpoints. The objective of the TSP is to determine a tour of minimum distance, i.e., to find the shortest path that visits each node exactly one time while starting and ending at the same node.

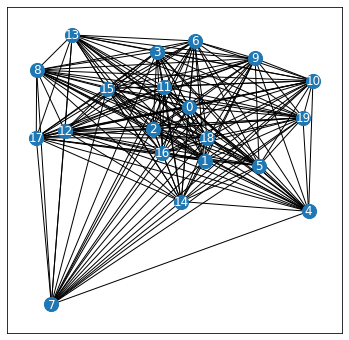
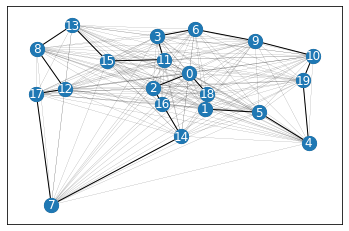
Below is an example of a NetworkX TSP problem with \(N=20\). Even for problem of this modest size, the number of TSP solutions is \(N! = 2,432,902,008,176,640,000 \approx 2 \times 10^{18}\).

[1]:

import matplotlib.pyplot as plt
from graphenv.examples.tsp.graph_utils import make_complete_planar_graph, plot_network

%matplotlib inline

[2]:

N = 20
G = make_complete_planar_graph(N, seed=0)

fig, ax = plot_network(G)
fig.set_size_inches(6, 6)

`graphenv` formulation

Note: In what follows, we assume the reader has already read and understood the HallwayEnv example as many of the basic graphenv concepts described in that example also apply here.

At a basic level, the TSP is readily modeled as a sequential decision-making problem where, at any point in the partial tour (solution), the agent decides which node to move to next. The action space is of variable length – in particular, the number of valid nodes decreases by 1 with each step because nodes can only be visited once – with an instantaneous step reward associated with each action, namely, the edge weight (distance) associated with moving from the current to the next node.

The figure below illustrates the decision-making process for a small instance (\(N=5\)) after an initial action has moved the agent from the originating node to a second node (blue circles). We denote this state of the graph search by \(s_1\). From this state, there are 3 remaining nodes (black circles) and associated edges (dashed lines) to choose from. By visual inspection, we can intuit that the action \(a_0(s_1)\) is better than either of the other actions, and would like our state representation to somehow encode this intuition so that the RL policy can learn to select it.

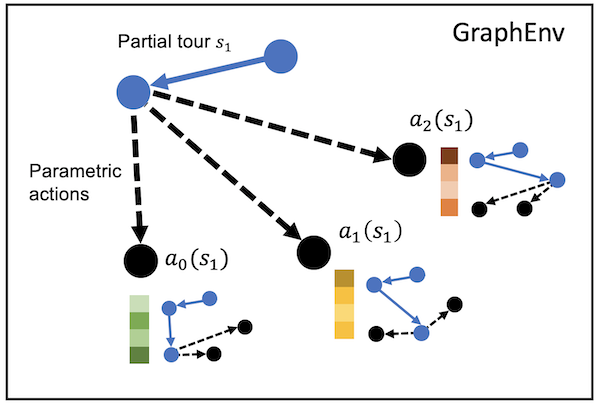
graphenv

As in the hallway example, the key to representing the TSP problem as a graphenv is to define the state representation (inheriting from the Vertex class) and an RL policy model that can ingest this representation. We walk through a very simple implementation here for the purpose of illustration, noting that getting SoTA performance will likely require a much more sophisticated state.

TSPState

(See graphenv.examples.tsp.tsp_state for the full implementation. A more advanced state implementation that uses graph neural network structure can be found in graphenv.examples.tsp.tsp_nfp_state).

`init`

Because the TSP problem has natural graph structure, our implementation utilizes a networkx graph to encode the problem instance. This is simply an implementation choice – any suitable data structure could be used here. The only required argument here is a graph generator, i.e., a callable function that returns a networkx graph. This is helpful when you want to solve the problem over a distribution of problem instances, e.g., with nodes distributed uniformly at random on the unit square. The init method also takes an optional graph instance, G (needed when creating child nodes), and list of previous visited nodes for when the TSPState represents an intermediate search state.

class TSPState(Vertex):
    """Create a TSP vertex that defines the graph search problem.

    Args:
        generator: a function that creates a networkx graph
        G: A fully connected networkx graph.
        tour: A list of nodes in visitation order that led to this
            state. Defaults to [0] which begins the tour at node 0.
    """

    def __init__(
        self,
        graph_generator: Callable[[], nx.Graph],
        G: Optional[nx.Graph] = None,
        tour: List[int] = [0],
    ) -> None:

        super().__init__()

        self.G = G if G is not None else graph_generator()
        self.num_nodes = self.G.number_of_nodes()
        self.tour = tour
        self.graph_generator = graph_generator

`_make_observation`

Next, we implement a simple observation space (not shown) and associated _make_observation method that defines the input features for the RL policy model. We emphasize that such a simple observation space is not likely to be competitive with SOTA methods for solving the TSP and serves only as illustration. The state dictionary consists of 4 features: the xy-position of the current node, its index, its distance to the previous node (if any), and the minimum distance to any available next node. Presumably, given a list of such child states, an RL policy could learn a greedy strategy that picks the child with, e.g., the shortest distance to its parent.

def _make_observation(self) -> Dict[str, np.ndarray]:
    """Return an observation.  The dict returned here needs to match
    both the self.observation_space in this class, as well as the input
    layer in tsp_model.TSPModel

    Returns:
        Observation dict.  We define the node_obs to be the degree of the
        current node.  This is a placeholder for a more meaningful feature!
    """

    cur_node = self.tour[-1]
    cur_pos = np.array(self.G.nodes[cur_node]["pos"], dtype=float).squeeze()

    # Compute distance to parent node, or 0 if this is the root.
    if len(self.tour) == 1:
        parent_dist = 0.0
    else:
        parent_dist = self.G[cur_node][self.tour[-2]]["weight"]

    # Get list of all neighbors that are unvisited.  If none, then the only
    # remaining neighbor is the root so dist is 0.
    nbrs = [n for n in self.G.neighbors(cur_node) if n not in self.tour]
    nbr_dist = 0.0
    if len(nbrs) > 0:
        nbr_dist = np.min([self.G[cur_node][n]["weight"] for n in nbrs])

    return {
        "node_obs": cur_pos,
        "node_idx": np.array([cur_node]),
        "parent_dist": np.array([parent_dist]),
        "nbr_dist": np.array([nbr_dist]),
    }

`reward`

We implement a reward for the TSP as the negative distance between the current and next nodes, offset by the greedy reward, i.e., the total reward found using greedy search. As a result, tours that perform worse than greedy have negative total rewards, and those that perform better have positive total rewards.

@property
def reward(self) -> float:
    """Returns the graph env reward.
    Returns:
        Negative distance between last two nodes in the tour.
    """

    if len(self.tour) == 1:
        # This should never be called
        rew = 0

    elif len(self.tour) >= 2:
        # Otherwise, reward is negative distance between last two nodes.
        src, dst = self.tour[-2:]
        rew = -self.G[src][dst]["weight"]

    else:
        raise RuntimeError(f"Invalid tour: {self.tour}")

    return rew

`_get_children`

Finally, our graphenv implementation requires that, for a given state, we can return a list of its children. There are two checks needed here:

The children should not include any previously visited states.
Whether we are at the next-to-last state, in which case our only option is to return to the starting state.

def _get_children(self) -> Sequence["TSPState"]:
    """Yields a sequence of TSPState instances associated with the next
    accessible nodes.
    Yields:
        New instance of the TSPState with the next node added to
        the tour.
    """
    G = self.G
    cur_node = self.tour[-1]

    # Look at neighbors not already on the path.
    nbrs = [n for n in G.neighbors(cur_node) if n not in self.tour]

    # Go back to the first node if we've visited every other already.
    if len(nbrs) == 0 and len(self.tour) == self.num_nodes:
        nbrs = [self.tour[0]]

    # Conditions for completing the circuit.
    if len(nbrs) == 0 and len(self.tour) == self.num_nodes + 1:
        nbrs = []

    # Loop over the neighbors and update paths.
    for nbr in nbrs:

        # Update the node path with next node.
        tour = self.tour.copy()
        tour.append(nbr)

        yield self.new(tour)

TSPModel

A simple Keras policy model for TSP is implemented here: graphenv.examples.tsp.tsp_model.

class BaseTSPModel(GraphModel):
    def __init__(
        self,
        *args,
        num_nodes: int,
        hidden_dim: int = 32,
        embed_dim: int = 32,
        **kwargs,
    ):
        super().__init__(*args, **kwargs)
        self.base_model = self._create_base_model(num_nodes, hidden_dim, embed_dim)

    @staticmethod
    def _create_base_model(
        num_nodes: int, hidden_dim: int = 32, embed_dim: int = 32
    ) -> tf.keras.Model:

        node_obs = layers.Input(shape=(2,), name="node_obs", dtype=tf.float32)
        node_idx = layers.Input(shape=(1,), name="node_idx", dtype=tf.int32)
        parent_dist = layers.Input(shape=(1,), name="parent_dist", dtype=tf.float32)
        nbr_dist = layers.Input(shape=(1,), name="nbr_dist", dtype=tf.float32)

        embed_layer = layers.Embedding(
            num_nodes, embed_dim, name="embed_layer", input_length=1
        )
        hidden_layer_1 = layers.Dense(
            hidden_dim, name="hidden_layer_1", activation="relu"
        )
        hidden_layer_2 = layers.Dense(
            hidden_dim, name="hidden_layer_2", activation="linear"
        )
        action_value_output = layers.Dense(
            1, name="action_value_output", bias_initializer="ones"
        )
        action_weight_output = layers.Dense(
            1, name="action_weight_output", bias_initializer="ones"
        )

        # Process the positional node data.  Here we need to expand the
        # middle axis to match the embedding output dimension.
        x = layers.Concatenate(axis=-1)([node_obs, parent_dist, nbr_dist])
        hidden = layers.Reshape((1, hidden_dim))(hidden_layer_1(x))

        # Process the embedding.
        embed = embed_layer(node_idx)

        # Concatenate and flatten for dense output layers.
        out = layers.Concatenate(axis=-1)([hidden, embed])
        out = layers.Flatten()(out)
        out = hidden_layer_2(out)

        # Action values and weights for RLLib algorithms
        action_values = action_value_output(out)
        action_weights = action_weight_output(out)

        return tf.keras.Model(
            [node_obs, node_idx, parent_dist, nbr_dist], [action_values, action_weights]
        )

TSPEnv Demo

Let’s look at a quick demo of creating and running the TSP environment. We’ll use the graph G from above as the problem instance, and compare a few baseline solution methods.

[3]:

import numpy as np
from graphenv.graph_env import GraphEnv
from graphenv.examples.tsp.tsp_state import TSPState

state = TSPState(graph_generator=lambda: G)
env = GraphEnv({"state": state, "max_num_children": N})

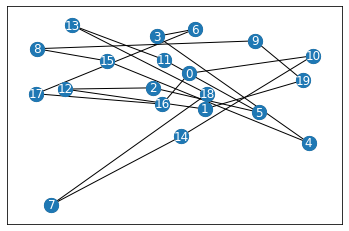
Solution Method: Random Tour

Recall that the reward here is how much worse than greedy.

[4]:

env.reset()

done = False
rand_rew = 0.
while not done:
    action = env.action_space.sample()
    _, rew, terminated, truncated, _ = env.step(action)
    done = terminated or truncated
    rand_rew += rew

print(f"Random reward = {rand_rew}")

path = env.state.tour
_ = env.render()

Random reward = -20.562185105071027

/Users/pstjohn/Packages/graph-env/graphenv/graph_env.py:110: RuntimeWarning: Attempting to choose a masked child state. This is either due to rllib's env pre_check module, or due to a failure of the policy model to mask invalid actions. Returning the current state to satisfy the pre_check module.
  warnings.warn(

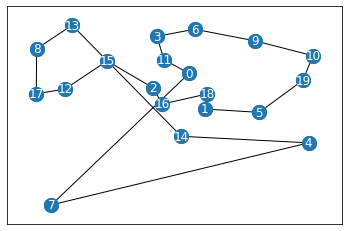
Solution Method: Greedy Search

Better than random, but still clearly not great.

[5]:

obs, info = env.reset()

done = False
greedy_rew = 0.
i = 0
while not done:
    # Get the node with shortest distance to the parent (current) node
    idx = np.argmin([x["parent_dist"] for x in obs[1:]])
    obs, rew, terminated, truncated, _ = env.step(idx)
    done = terminated or truncated
    greedy_rew += rew

print(f"Greedy reward = {greedy_rew}")

path = env.state.tour
_ = env.render()

Greedy reward = -5.3454995624259976

Solution Method: networkx heuristics

Just for fun, because we implemented the problem instance in networkx, we can use the library’s built-in heuristics for solving TSP outsid of graphenv. Note there is no RL being applied here – you need graphenv for that – but the heuristics provide strong benchmarks to compare against.

[6]:

import networkx as nx

path = nx.approximation.traveling_salesman.christofides(G)
_ = plot_network(G=G, path=path)

Policy Training

See tests/test_tsp.py for some simple examples of training the policy with RLLib.